Maximize Distance to Closest Person LeetCode Solution

Problem Statement

Maximize Distance to Closest Person LeetCode Solution – You are given an array representing a row of seats where seats[i] = 1 represents a person sitting in the i^th seat, and seats[i] = 0 represents that the i^th seat is empty (0-indexed).

There is at least one empty seat, and at least one person sitting.

Alex wants to sit in the seat such that the distance between him and the closest person to him is maximized.

Return that maximum distance to the closest person.

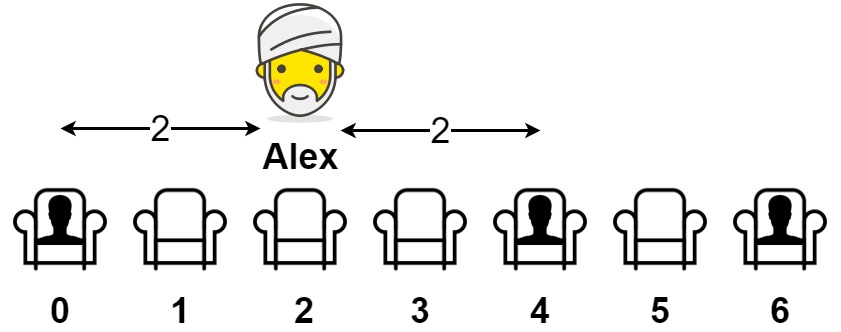
Input: seats = [1,0,0,0,1,0,1]
Output: 2
Explanation: 
If Alex sits in the second open seat (i.e. seats[2]), then the closest person has distance 2.
If Alex sits in any other open seat, the closest person has distance 1.
Thus, the maximum distance to the closest person is 2.

Explanation

last is the index of the last seated seat.
Loop on all seats, when we met a people, we count the distance from the last.
The final result = max(distance at the beginning, distance in the middle / 2, distance at the end).

If Alex sits on the 1st seat the closet neighbour will be at a distance of 1 from his left. But let’s say if Alex sits on the 2nd seat the closet neighbour will be at a distance of 2 from his left & from his right as well. But again let’s say Alex sits on the 3rd seat the closet neighbour will be at a distance of 1 from his right. But again let’s say Alex sits on the 5th seat the closet neighbour will be at a distance of 1 from his left & from his right as well.
So, the distances we get from all 4 seating from the different neighbours is [1, 2, 1, 1] and the maximum one is 2. So, Alex will prefer to sit over 2nd seat. So, that he doesn’t get COVID.

So, how will we arrive at this solution, there are 2 possibilities :

1. Alex can sit on internal chairs. Excluding 1st or last
2. Edges [Alex can sit on 1st OR last seat]

So, let's understand 1st possibilitiy.

• So, 1st and last are occupied and in the middle, we have 3 consecutive zeros followed by 1 and let’s say again 2 consecutive zeros. If any 1 occurs we can think of it as a separator. So, for 3 consecutive zeros, the nearest neighbour’s maximum value will be 2.
• Similar to 4 consecutive zeros the nearest neighbour’s maximum value will be 2.
• When we have 2 consecutive zeros the nearest neighbour’s maximum value will be 1.
• And similar to 1 consecutive zeros the nearest neighbour’s maximum value will be 1.

By looking at this possibility the formula we can generate is n + 1 / 2.

So, these are the cases when Alex sits on Internal chairs.

Now, when Alex sit on edges.

• So, let’s say in the starting we have 3 consecutive zeros followed by 1 and let’s say again 4 consecutive zeros followed by 1. So, for 3 consecutive zeros in the starting, the nearest neighbour maximum value will be 3.
• But let’s say we have 1 in starting followed by 3 consecutive zeros then 1 and let’s say again 4 consecutive zeros. So, for 4** consecutive zeros** in the end the nearest neighbour maximum value will be 4.

By looking at this possibility the formula we can generate for consecutive zeros on left is idx1 & for consecutive zeros on right is n - 1 - idx2 [where idx is index]

So, whatever the maximum value we get from Internal & edges we will consider it to be the nearest neighbour maximum value where Alex can sit.

Code

C++ Code for Maximize Distance to Closest Person

class Solution {
public:
     int maxDistToClosest(vector<int> seats) {
        int res = 0, n = seats.size(), last = -1;
        for (int i = 0; i < n; ++i) {
            if (seats[i] == 1) {
                res = last < 0 ? i : max(res, (i - last) / 2);
                last = i;
            }
        }
        res = max(res, n - last - 1);
        return res;
    }
};

Java Code for Maximize Distance to Closest Person

class Solution {
    public int maxDistToClosest(int[] seats) {
        int res = 0, n = seats.length, last = -1;
        for (int i = 0; i < n; ++i) {
            if (seats[i] == 1) {
                res = last < 0 ? i : Math.max(res, (i - last) / 2);
                last = i;
            }
        }
        res = Math.max(res, n - last - 1);
        return res;
    }
}

Python Code for Maximize Distance to Closest Person

class Solution:
    def maxDistToClosest(self, seats):
        res, last, n = 0, -1, len(seats)
        for i in range(n):
            if seats[i]:
                res = max(res, i if last < 0 else (i - last) / 2)
                last = i
        return max(res, n - last - 1)

Complexity Analysis for Maximize Distance to Closest Person LeetCode Solution

Time Complexity

O(n)

Space Complexity

O(1)