Maximum Depth of N-ary Tree Leetcode Solution

In this problem, we are given an N-ary tree, that is, a tree that allows nodes to have more than 2 children. We need to find the depth of a leaf farthest from the root of the tree. This is called maximum depth. Note that the depth of a path is the number of nodes on it.

Table of Contents

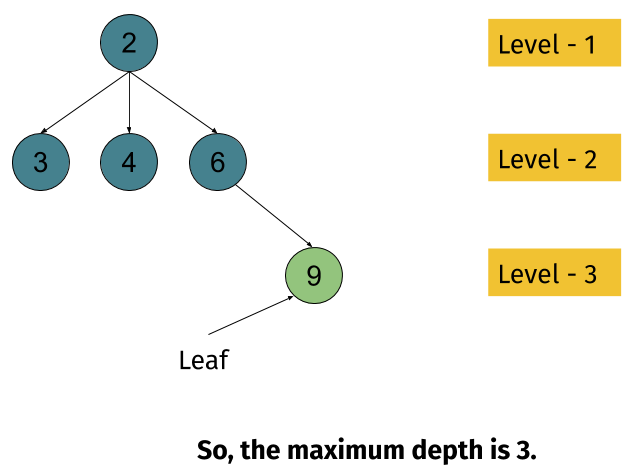
Example

       2

  /    |    \

3      4      6

                \
           
                  9

Explanation: The leaf with value 9 is farthest from the root and its depth is 3. So, we print 3.

      2
  
  /      \

3           6   

        /   |   \

      4     7     9

Explanation: The leaves with value 4,7 and 9 are farthest from the root and their depth is 3. So, we print 3.

Approach(Recursive)

The maximum depth of a binary tree is calculated by calling the recursive function on left and right children of any node. Similarly, in case of an N-ary tree, we can calculate the maximum depth by calling the recursive function on all the children of any node. This approach is recursive and requires only a single pass of the tree.

Algorithm

Create a function maxDepth() to return the maximum depth of a tree whose root is passed to it
If root is null:
- return 0
Initialize a variable maximumDepth to store the maximum depth of N-ary tree
For every child in the children list of the current root:
- set maximumDepth = max(maxDepth(root.left) , maxDepth(root.right))
return maximumDepth + 1

Implementation of Maximum Depth of N-ary Tree Leetcode Solution

C++ Program

#include <bits/stdc++.h>
using namespace std;

struct Node
{
    int value;
    vector <Node*> children;

    Node(int val)
    {
        value = val;
        children = {};
    }

    Node(int val , vector <Node*> childList)
    {
        value = val;
        children = childList;
    }
};

int maxDepth(Node* root)
{
    if(root == NULL)
        return 0;
    int maximumDepth = 0;
    for(Node* &child : root->children)
        maximumDepth = max(maximumDepth , maxDepth(child));
    return maximumDepth + 1;
}

int main()
{
    Node* root = new Node(2);
    root->children = {new Node(3) , new Node(4) , new Node(5)};
    root->children[2]->children = {new Node(9)};
    cout << maxDepth(root) << '\n';
    return 0;
}

Java Program

import java.lang.Math;

class Node
{
    int value;
    Node[] children;

    Node(int val)
    {
        value = val;
        children = new Node[]{};
    }

    Node(int val , Node[] childList)
    {
        value = val;
        children = childList;
    }
};

class maximum_depth
{
    public static void main(String args[])
    {
        Node root = new Node(2);
        Node[] a = {new Node(3) , new Node(4) , new Node(5)};
        root.children = a;
        Node[] b = {new Node(9)};
        root.children[2].children = b;
        System.out.println(maxDepth(root));
    }

    static int maxDepth(Node root)
    {
        if(root == null)
            return 0;
        int maximumDepth = 0;
        for(int i = 0 ; i < root.children.length ; i++)
            maximumDepth = Math.max(maximumDepth , maxDepth(root.children[i]));
        return maximumDepth + 1;
    }
}

Complexity Analysis of Maximum Depth of N-ary Tree Leetcode Solution

Time Complexity

O(N), N = size of the N-ary tree as we traverse the whole tree once.

Space Complexity

O(N) as we store stack frames in the memory for recursive calls.

Approach(Iterative)

We can do the above process iteratively by using either a stack or a queue to store nodes and their depths from the root. The maximum depth will be the maximum of depths of all roots obtained from this process. We use a queue for this purpose and push all the elements of the tree into the queue along with their depths from the root. We compare the depth of every node with the maximum depth and update it.

Algorithm

Create the function maxDepth() similar as discussed in the above approach
If root is null:
- return 0
Initialise maximumDepth to store our result
Initialise a queue elements that contains tree nodes and their depths
Push root and its depth as 1 into the queue
While elements is not empty:
- Fetch the front node and its height as frontNode and frontNodeDepth
- Pop an item out of the queue
- If frontNodeDepth is greater than maximumDepth
  1. Update maximumDepth = frontNodeDepth
- If frontNode is not null:
  1. Push all its children into the queue with their depths as frontNodeDepth + 1
return maximumDepth
Print the result

Implementation of Maximum Depth of N-ary Tree Leetcode Solution

C++ Program

#include <bits/stdc++.h>
using namespace std;

struct Node
{
    int value;
    vector <Node*> children;

    Node(int val)
    {
        value = val;
        children = {};
    }

    Node(int val , vector <Node*> childList)
    {
        value = val;
        children = childList;
    }
};

int maxDepth(Node* root)
{
    if(root == NULL)
        return 0;
    int maximumDepth = 0 , frontNodeDepth;

    queue <pair <Node* , int> > elements;
    elements.push({root , 1});
    Node* frontNode;
    while(!elements.empty())
    {
        frontNode = elements.front().first;
        frontNodeDepth = elements.front().second;
        elements.pop();
        if(frontNodeDepth > maximumDepth)
            maximumDepth = frontNodeDepth;

        if(frontNode != NULL)
        {
            for(Node* &child : frontNode->children)
                elements.push({child , frontNodeDepth + 1});
        }
    }

    return maximumDepth;
}

int main()
{
    Node* root = new Node(2);
    root->children = {new Node(3) , new Node(4) , new Node(5)};
    root->children[2]->children = {new Node(9)};
    cout << maxDepth(root) << '\n';
    return 0;
}

Java Program

import java.lang.Math;
import java.util.*;

class Node
{
    int value;
    Node[] children;

    Node(int val)
    {
        value = val;
        children = new Node[]{};
    }

    Node(int val , Node[] childList)
    {
        value = val;
        children = childList;
    }
};

class Pair
{
    Node key;
    int value;
    Pair(Node root , int val)
    {
        key = root;
        value = val;
    }
}

class maximum_depth
{
    public static void main(String args[])
    {
        Node root = new Node(2);
        Node[] a = {new Node(3) , new Node(4) , new Node(5)};
        root.children = a;
        Node[] b = {new Node(9)};
        root.children[2].children = b;
        System.out.println(maxDepth(root));
    }

    static int maxDepth(Node root)
    {
        if(root == null)
            return 0;
        LinkedList <Pair> elements = new LinkedList <>();
        elements.add(new Pair(root , 1));
        Node frontNode;
        int maximumDepth = 0 , frontNodeDepth;

        while(elements.size() > 0)
        {
            frontNode = elements.peek().key;
            frontNodeDepth = elements.peek().value;
            elements.remove();
            if(frontNodeDepth > maximumDepth)
                maximumDepth = frontNodeDepth;

            if(frontNode != null)
            {
                for(int i = 0 ; i < frontNode.children.length ; i++)
                    elements.add(new Pair(frontNode.children[i] , frontNodeDepth + 1));
            }
        }
        return maximumDepth;
    }
}