Maximum Nesting Depth of the Parentheses Leetcode Solution

Difficulty Level Easy
Frequently asked in Bloomberg
algorithms coding Interview interviewprep LeetCode LeetCodeSolutions StringViews 3486

Problem Statement

In this problem, we are given a valid parentheses string (vps) having some numbers, some operators(e.g. +,-,*) and some parentheses(e.g. ‘(‘,’)’).
Valid parentheses strings (vps) are:

  1.  “”
  2. “d” where d is any number
  3. “(A)” if A is valid parentheses string
  4. “A*B” if * is any operator and A and B are valid parentheses string.

Our aim is to find the maximum depth of the parentheses in the given string.
e.g. “(1+(2*3)+((8)/4))+1”
we can see that at the number 8 is inside the maximum number of parentheses and the depth of parentheses there is 3. We will output 3.

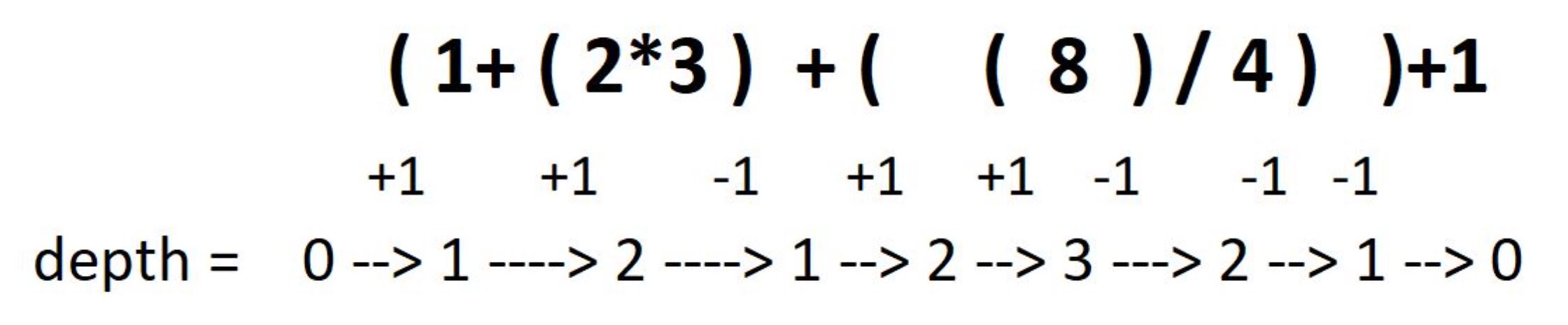
Maximum Nesting Depth of the Parentheses Leetcode Solution
Let’s see one more example,
e.g. “1+(2*3)/(2-1)”
the vps 2*3 or another vps 2-1, both are inside the maximum depth of parentheses i.e. 1.

Example

s = "(1+(2*3)+((8)/4))+1"
3

Explanation:

Digit 8 is inside of 3 nested parentheses in the string.

s = "(1)+((2))+(((3)))"
3

Approach

We are given that the string is a vps and we just have to find out the maximum depth of parentheses. So, we can just focus on the parentheses and ignore other characters (numbers and operators).

The depth of parentheses increase only when there starts a new nested parentheses. i.e. the starting parentheses ‘(‘ means that depth of parentheses increase by 1. And when the parentheses is closed, then depth decreases by 1. i.e. ‘)’ means depth is decreased by 1.

In our approach we will just use a current depth variable (let k) and a maximum depth variable (let ans).Both are initialized to 0 (depth 0 means we are out of all parentheses initially). And start traversing the input string from left to right. According to the trick we discussed, whenever we will encounter a ‘(‘ sign we will increase current depth k by 1 and whenever we will encounter a ‘)’ sign we will decrease current depth k by 1.
Each time we will check if the current depth greater than maximum depth. If yes then we will assign current depth to the maximum depth variable.
Finally after the traversal, our ans variable has stored the maximum depth, hence we will output it.

Implementation

C++ Program for Maximum Nesting Depth of the Parentheses Leetcode Solution

#include <iostream>
using namespace std;

int maxDepth(string s) 
{
    int ans=0,k=0;
    for(int i=0;i<s.length();i++)
    {
        if(s[i]=='(')k++;
        else if(s[i]==')')k--;
        ans=ans>k?ans:k;
    }
    return ans;
}
int main()
{
    cout<<maxDepth("(1)+((2))+(((3)))");
}
3

Java Program for Maximum Nesting Depth of the Parentheses Leetcode Solution

import java.util.*;
import java.lang.*;

class Solution
{  
    public static int maxDepth(String s) 
    {
        int ans=0,k=0;
        for(int i=0;i<s.length();i++)
        {
            if(s.charAt(i)=='(')k++;
            else if(s.charAt(i)==')')k--;
            ans=Math.max(ans,k);
        }
        return ans;
    }
    
    public static void main(String args[])
    {
        System.out.println(maxDepth("(1)+((2))+(((3)))"));
    }
}
3

Complexity Analysis for Maximum Nesting Depth of the Parentheses Leetcode Solution

Time Complexity

O(n): We are traversing the given expression from left to right. Thus it is O(n) where n is length of the given string.

Space Complexity 

O(1): We haven’t used constant extra spaces. Thus space complexity is O(1).

Translate »