The problem Minimum Distance Between BST Nodes Leetcode Solution states that you are provided with a Binary Search Tree. And you are required to find the minimum difference in the entire BST. So, you need to find the minimum absolute difference between any two nodes in the BST. A BST or a Binary Search Tree is nothing but a tree with some nodes that follow a rule. the rule is that the left subtree of a node must contain only the nodes that have a value less than the current node. Similarly, for the right subtree, the nodes must contain values greater than the current node. So, as usual, we must first take a look at a few examples before jumping into the solution.
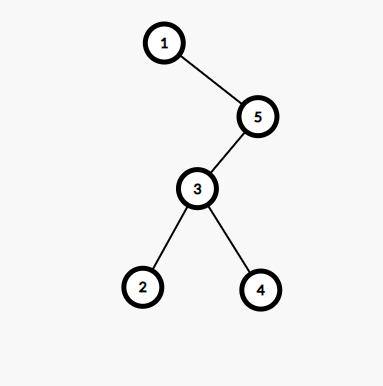
1
Explanation: The difference between the nodes [1, 2], [2, 3], [3, 4], [4, 5] all have difference of 1. And all other pairs have a greater difference. Thus the answer is 1.
Table of Contents
Brute Force Approach for Minimum Distance Between BST Nodes Leetcode Solution
The problem Minimum Distance Between BST Nodes Leetcode Solution asked us to find the minimum difference between any two nodes in a given Binary Search Tree. So, one way to find the answer is to pick any two vertices or nodes of the BST and calculate the difference. We will update the answer once we find a pair that has a lesser absolute difference than the previous pair. Initially, we can use any two nodes, and at the end of the process. The answer will be stored in the respective variables. So, to simulate this process, we will traverse the BST in an inorder manner and store it in a vector. Using two nested loops, we will keep on calculating the absolute difference between every two vertices in the tree.
Brute Force Code
C++ code for Minimum Distance Between BST Nodes Leetcode Solution
#include <bits/stdc++.h>
using namespace std;
struct TreeNode{
int val;
TreeNode *left, *right;
};
vector<int> inorder_traversal;
int ans = INT_MAX;
void inorder(TreeNode* root){
if(root){
inorder(root->left);
inorder_traversal.push_back(root->val);
inorder(root->right);
}
}
int minDiffInBST(TreeNode* root) {
inorder(root);
for(int i=1;i<inorder_traversal.size();i++)
ans = min(ans, inorder_traversal[i]-inorder_traversal[i-1]);
return ans;
}
int main(){
TreeNode* root = new TreeNode();
root->val = 1;
root->right = new TreeNode();
root->right->val = 5;
root->right->left = new TreeNode();
root->right->left->val = 3;
root->right->left->left = new TreeNode();
root->right->left->left->val = 2;
root->right->left->right = new TreeNode();
root->right->left->right->val = 4;
cout<<minDiffInBST(root);
}1
Java code for Minimum Distance Between BST Nodes Leetcode Solution
import java.util.*;
import java.lang.*;
import java.io.*;
class TreeNode{
int val;
TreeNode left;
TreeNode right;
}
class Main {
static ArrayList<Integer> inorder_traversal = new ArrayList<Integer>();
static int ans = Integer.MAX_VALUE;
public static void inorder(TreeNode root){
if(root != null){
inorder(root.left);
inorder_traversal.add(root.val);
inorder(root.right);
}
}
public static int minDiffInBST(TreeNode root) {
inorder(root);
for(int i=1;i<inorder_traversal.size();i++)
ans = Math.min(ans, inorder_traversal.get(i)-inorder_traversal.get(i-1));
return ans;
}
public static void main (String[] args) throws java.lang.Exception
{
TreeNode root = new TreeNode();
root.val = 1;
root.right = new TreeNode();
root.right.val = 5;
root.right.left = new TreeNode();
root.right.left.val = 3;
root.right.left.left = new TreeNode();
root.right.left.left.val = 2;
root.right.left.right = new TreeNode();
root.right.left.right.val = 4;
System.out.print(minDiffInBST(root));
}
}1
Complexity Analysis
Time Complexity
O(N^2), since we have used 2 nested loops to find the minimum absolute difference, the time complexity for this approach becomes polynomial.
Space Complexity
O(N), because we had to store the inorder traversal in a vector or an array. Thus, the space complexity is linear.
Optimized Approach for Minimum Distance Between BST Nodes Leetcode Solution
The above approach for the problem inorder traversal. Not only it used inorder traversal, but it also stored it, making the approach O(N) in terms of space complexity. We also did not use the fact that we had a BST, and the minimum absolute difference can only be obtained between two consecutive vertices. Because of fact not taken into account, we had a polynomial time complexity.
In the optimized approach, we keep track of the previous node to the current vertex. Doing this helps us to find the minimum absolute difference by performing evaluation operation only N-1 times. This also helps us to achieve constant space complexity because we do not have to store the entire inorder traversal, and store only the previous node.
Optimized code for Minimum Distance Between BST Nodes Leetcode Solution
C++ code
#include <bits/stdc++.h>
using namespace std;
struct TreeNode{
int val;
TreeNode *left, *right;
};
TreeNode* previous = NULL;
int ans = INT_MAX;
void inorder(TreeNode* root){
if(root){
inorder(root->left);
if(previous != NULL){
ans = min(ans, root->val - previous->val);
}
previous = root;
inorder(root->right);
}
}
int minDiffInBST(TreeNode* root) {
inorder(root);
return ans;
}
int main(){
TreeNode* root = new TreeNode();
root->val = 1;
root->right = new TreeNode();
root->right->val = 5;
root->right->left = new TreeNode();
root->right->left->val = 3;
root->right->left->left = new TreeNode();
root->right->left->left->val = 2;
root->right->left->right = new TreeNode();
root->right->left->right->val = 4;
cout<<minDiffInBST(root);
}1
Java Code
import java.util.*;
import java.lang.*;
import java.io.*;
class TreeNode{
int val;
TreeNode left;
TreeNode right;
}
class Main {
static TreeNode prev = null;
static int ans = Integer.MAX_VALUE;
public static void inorder(TreeNode root){
if(root != null){
inorder(root.left);
if(prev != null){
ans = Math.min(ans, root.val - prev.val);
}
prev = root;
inorder(root.right);
}
}
public static int minDiffInBST(TreeNode root) {
inorder(root);
return ans;
}
public static void main (String[] args) throws java.lang.Exception
{
TreeNode root = new TreeNode();
root.val = 1;
root.right = new TreeNode();
root.right.val = 5;
root.right.left = new TreeNode();
root.right.left.val = 3;
root.right.left.left = new TreeNode();
root.right.left.left.val = 2;
root.right.left.right = new TreeNode();
root.right.left.right.val = 4;
System.out.print(minDiffInBST(root));
}
}1
Complexity Analysis
Time Complexity
O(N), since we used only inorder traversal which traversed over the N nodes on the tree. Thus the time complexity is linear.
O(1), since we used only a constant number of variables. Space complexity also reduced to constant space.