Table of Contents
Problem Statement
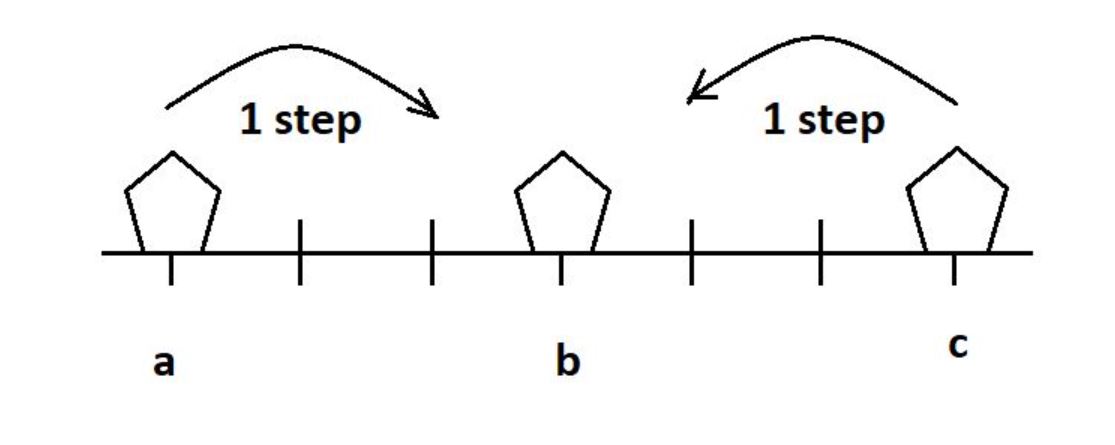
In this problem, we are given three stones at positions a, b and c. We have to make them consecutive by performing the following step one or more times.
In each step, We will pick a left stone or a right stone and put somewhere in the between the range of left to right stone.
Let’s under stand this better by following picture:
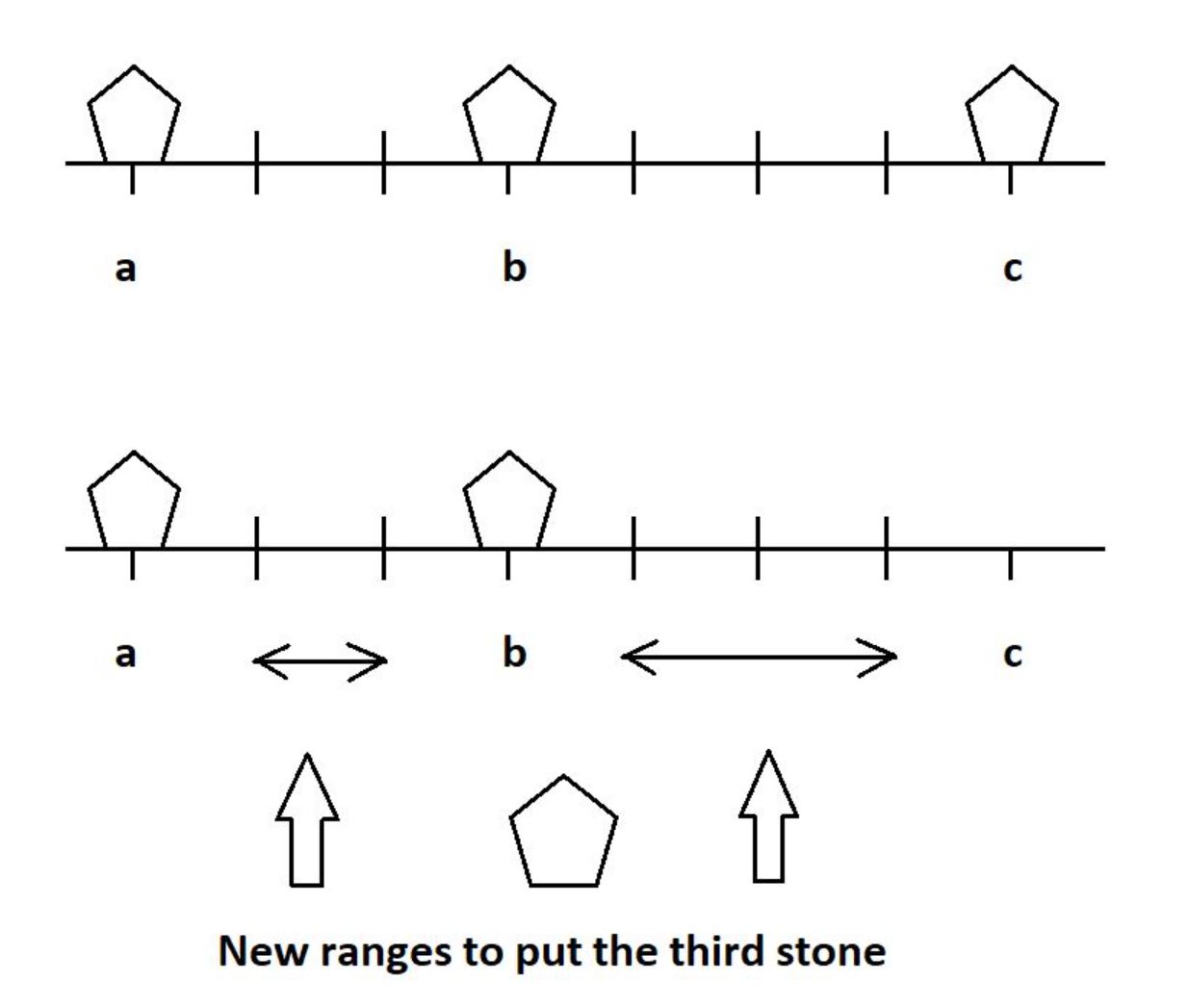
We have to answer both the minimum and maximum number of such steps to make these stones consecutive.
Example
a = 1, b = 2, c = 5
[1,2]
Explanation: Move the stone from 5 to 3, or move the stone from 5 to 4 to 3.
a = 4, b = 3, c = 2
[0,0]
We cannot make any moves.
a = 3, b = 5, c = 1
[1,2]
Move the stone from 1 to 4; or move the stone from 1 to 2 to 4.
Approach
First let’s talk about how to calculate maximum steps. Can’t we simply say that the number of moves will be maximum only when both the stones at extremes come closer to middle stone by 1 unit.
Thus the number of positions between left stone and mid stone + the number of position between mid stone and right stone will be our maximum number of steps to make them consecutive.

Now the main problem is how to calculate minimum number of steps. We can find out minimum by understanding the following conditions.
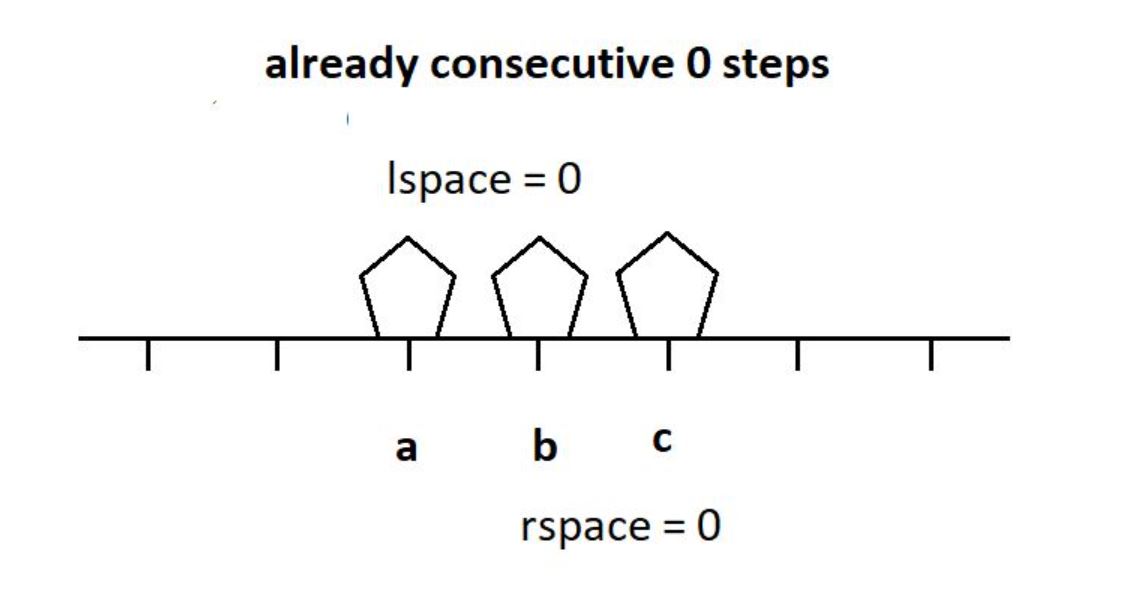
Let’s call number of positions between left stone and mid stone is lspace and the number of positions between mid stone and right stone is rspace.
Only one of the following 4 situation can be said about the initial position of these stones.
1. If the stones are already consecutive i.e. lspace=0 and rspace=0 then min_steps=0.
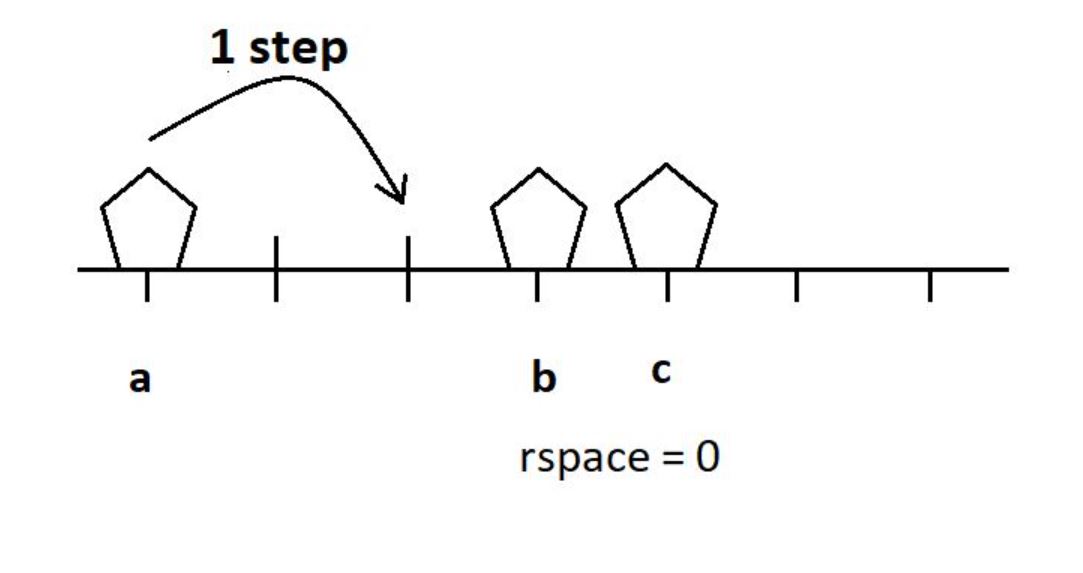
 2. Else if two of the three stones are consecutive i.e. if lspace=0 or rspace=0 then we can simply put far most stone at near to the mid stone in just 1 step thus min_steps=1.
2. Else if two of the three stones are consecutive i.e. if lspace=0 or rspace=0 then we can simply put far most stone at near to the mid stone in just 1 step thus min_steps=1.
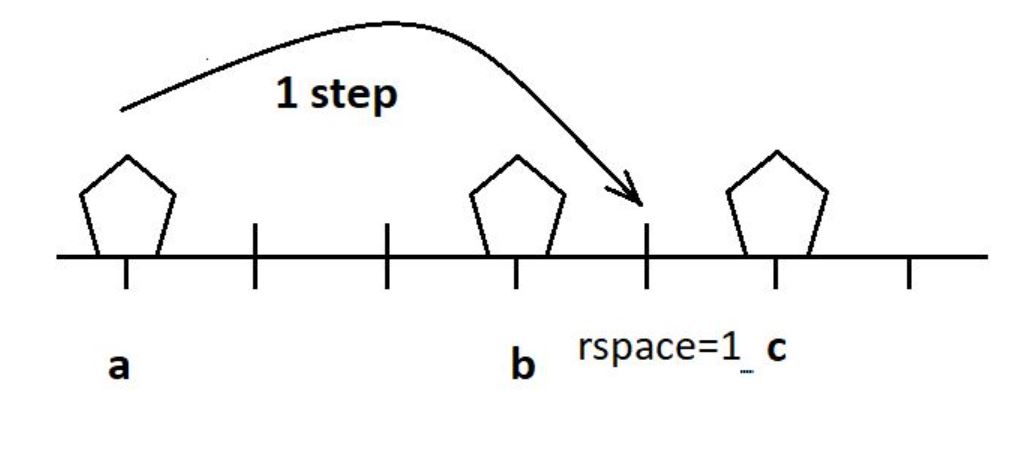
 3. Else if the space between any two of the three stones is 1 i.e. if lspace=1 or rspace=1. Then, the far most stone can be put between two near stones (note that near stones have just one position between them) in just a single step.
3. Else if the space between any two of the three stones is 1 i.e. if lspace=1 or rspace=1. Then, the far most stone can be put between two near stones (note that near stones have just one position between them) in just a single step.
Hence, making them consecutive can happen in just 1 step. Thus, min_steps=1.
 4. Else the stones at both extreme can be put in neighbour of mid stones by 1 step each. Thus, min_steps=1+1=2.
4. Else the stones at both extreme can be put in neighbour of mid stones by 1 step each. Thus, min_steps=1+1=2.
Implementation
C++ Program for Moving Stones Until Consecutive Leetcode Solution
#include <bits/stdc++.h>
using namespace std;
vector<int> numMovesStones(int a, int b, int c)
{
int left=min(a,min(b,c));
int right=max(a,max(b,c));
int mid=(a!=left && a!=right )?a:(b!=left && b!=right)?b:c;
int lspace=mid-left-1;
int rspace=right-mid-1;
int max=lspace+rspace,min=0;
if(lspace==0 && rspace==0)min=0;
else if(lspace==0 || rspace==0)min=1;
else if(lspace==1 || rspace==1)min=1;
else min=2;
vector<int> ans{min,max};
return ans;
}
int main()
{
vector<int>ans=numMovesStones(1,2,5);
cout<<ans[0]<<" "<<ans[1]<<endl;
}1 2
Java Program for Moving Stones Until Consecutive Leetcode Solution
#include <bits/stdc++.h>
using namespace std;
vector<int> numMovesStones(int a, int b, int c)
{
int left=min(a,min(b,c));
int right=max(a,max(b,c));
int mid=(a!=left && a!=right )?a:(b!=left && b!=right)?b:c;
int lspace=mid-left-1;
int rspace=right-mid-1;
int max=lspace+rspace,min=0;
if(lspace==0 && rspace==0)min=0;
else if(lspace==0 || rspace==0)min=1;
else if(lspace==1 || rspace==1)min=1;
else min=2;
vector<int> ans{min,max};
return ans;
}
int main()
{
vector<int>ans=numMovesStones(1,2,5);
cout<<ans[0]<<" "<<ans[1]<<endl;
}1 2
Complexity Analysis for Moving Stones Until Consecutive Leetcode Solution
Time Complexity
O(1) : We have just used simple conditional statements in our algorithm. Thus, the time complexity is O(1).
Space Complexity
O(1) : Apart from variables like left, right, lspace , ans array of size 2 etc., we haven’t created any extra space thus space complexity too is O(1).