Partition List Leetcode Solution

Difficulty Level Medium
Frequently asked in Adobe Amazon Apple Bloomberg Facebook MicrosoftViews 869

Problem Statement :

Partition List Leetcode Solution – Given the head of a linked list and a value x, partition it such that all nodes less than x come before nodes greater than or equal to x.

You should preserve the original relative order of the nodes in each of the two partitions.

Example :

Example 1 

Partition List Leetcode Solution

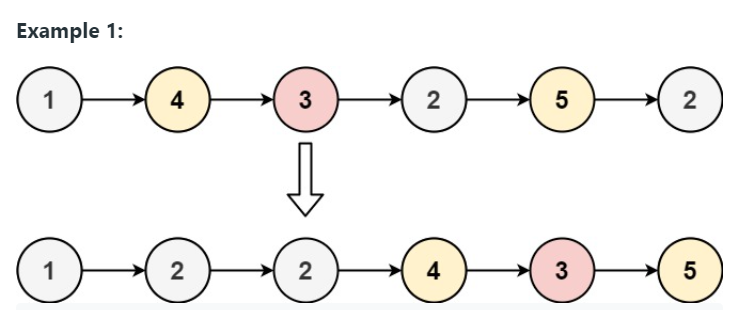
Input: head = [1,4,3,2,5,2], x = 3
Output: [1,2,2,4,3,5]

Example 2

Input: head = [2,1], x = 2
Output: [1,2]

Constraints :

Partition List Leetcode Solution

 

Explanation :

  • Given the head of a linked list and a value x.
  • We need to partition or reorder the list so that all nodes less than x come before nodes greater than or equal to x.
  • We should preserve the original relative order of the nodes in each of the two partitions.
  • From the Example 1, the First partition [1 -> 2 -> 2], the Second partition [4 -> 3 -> 5].
  • As we can see all the nodes that have a value less than x appear before the second partition, also the relative order is preserved on both partitions.

Intuition :

  • We will make two pointers dummyOne and dummyTwo.
  • These two pointers keep track of the two linked lists as described above.
  • These two pointers could be used two create two separate lists and then these lists could be combined to form the desired reformed list.
  • dummyOne will contain the first partition [ 1 -> 2 -> 2 ].
  • dummyTwo will contain the second partition [4 -> 3 -> 5] .
  • At last we will join the dummyOne and dummyTwo and return the desired reformed list  [1 -> 2 -> 2 -> 4 -> 3 -> 5 ].

Algorithm :

  • Initialize two pointers dummyOne and dummyTwo.
  • In the algorithm, we initialize these two pointers with a dummy ListNode, because using a dummy ListNode helps us reduce the number of conditional checks and null pointer exceptions.

  • We will also maintain the tail node of the dummy list node, it will help us to add at the end of the dummy node.

  • Iterate the original linked list, using the curr pointer.

  • Now

  • If the curr node’s value is lesser than X, then remove that node from the original list and add it at Last in the dummyOne list.

  • Otherwise, the node should be part of dummyTwo list. So we add that curr node in dummyTwo list at the end.

  • Once we are done with all the nodes in the original linked list, we would have two lists dummyOne and dummyTwo.

  • Now, these two lists dummyOne and dummyTwo can be combined to form the reformed list.

Code for Partition List :

Java  Code 

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode partition(ListNode head, int x) {
        
        ListNode dummyOne=new ListNode(-1);
        ListNode dummyTwo=new ListNode(-1);
        ListNode tailOne=dummyOne;
        ListNode tailTwo=dummyTwo;
        ListNode curr=head;
        while(curr!=null){
           ListNode temp=curr;
            curr=curr.next;
            temp.next=null;
            if(temp.val<x){
               tailOne= addNodeAtLast(temp,tailOne);
               
            }
            else{
              tailTwo=  addNodeAtLast(temp,tailTwo);
            }
        }
        tailOne.next=dummyTwo.next;
        return dummyOne.next;
    }
//------ Add Node At Last -------------   
    public ListNode addNodeAtLast(ListNode node, ListNode tail){
        tail.next=node;
        tail=tail.next;
        return tail;
    }

}

C++  Code

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* partition(ListNode* head, int x) {
          ListNode* dummyOne=new ListNode(-1);
        ListNode* dummyTwo=new ListNode(-1);
        ListNode* tailOne=dummyOne;
        ListNode* tailTwo=dummyTwo;
        ListNode* curr=head;
        while(curr!=NULL){
           ListNode* temp=curr;
            curr=curr->next;
            temp->next=NULL;
            if(temp->val<x){
               tailOne= addNodeAtLast(temp,tailOne);
               
            }
            else{
              tailTwo=  addNodeAtLast(temp,tailTwo);
            }
        }
        tailOne->next=dummyTwo->next;
        return dummyOne->next;
    }
//------ Add Node At Last -------------   
     ListNode* addNodeAtLast(ListNode* node, ListNode* tail){
        tail->next=node;
        tail=tail->next;
        return tail;
    }
    
};

Complexity Analysis for Partition List Leetcode Solution:

Time Complexity

 O(N), where N is the number of nodes in the original linked list and we iterate the original list.

Space Complexity 

O(1), we have not utilized any extra space.

Translate »