Perfect Squares LeetCode Solution

Problem Statement

The Perfect Squares LeetCode Solution – “Perfect Squares” states that given an integer n and you need to return the minimum number of perfect squares whose sum equals to n. Note that the same perfect square can be used multiple times.

Example:

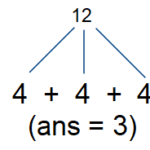
Input: n = 12

Output: 3

Explanation:

• We can use three times 4 to get the sum 12, so the answer is 3 which is the minimum.
• Note that the same perfect square can be used multiple times.

Input: n = 13

Output: 2

Explanation:

• We can use one times 4 and one times 9 to get a sum of 13, so the answer is 2 which is the minimum possible.

Approach

Idea:

1. The main idea is to use dynamic programming to solve this problem efficiently.
2. Consider the state of the dp as, dp[i] = minimum number of perfect squares that sum to i.
3. For each, i in the range [1,n] and, for each perfect square j less than or equal to i, if dp[i-j*j] exists, update dp[i] = min(dp[i],1+dp[i-j*j]), since we can reach the state i from (i-j*j) number by using j*j as the perfect square.
4. Our answer will be dp[n], the minimum number of perfect squares that sum to n.

Code

Perfect Squares Leetcode C++ Solution:

class Solution {
public:
    int numSquares(int n) {
        vector<int> perfectSquares;
        for(int i=1;i*i<=n;i++){
            perfectSquares.push_back(i*i);
        }
        vector<int> dp(n+1,INT_MAX);
        dp[0] = 0;
        for(int i=1;i<=n;i++){
            for(auto& j:perfectSquares){
                if(j<=i && dp[i-j]!=INT_MAX){
                    dp[i] = min(dp[i],1+dp[i-j]);
                }
            }
        }
        return dp[n];
    }
};

Perfect Squares Leetcode Java Solution:

class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n+1];
        dp[0] = 0;
        for(int i=1;i<=n;i++){
            dp[i] = Integer.MAX_VALUE;
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j*j<=i;j++){
                int square_integer = j*j;
                if(dp[i-square_integer]!=Integer.MAX_VALUE){
                    dp[i] = Math.min(dp[i],1+dp[i-square_integer]);
                }
            }
        }
        return dp[n];
    }
}

Complexity Analysis for Perfect Squares Leetcode Solution

Time Complexity

The time complexity of the above code is O(n*sqrt(n)) since the outer loop runs exactly n times and the inner loop runs sqrt(n) time in the worst case to find all perfect squares.

Space Complexity

The space complexity of the above code is O(n) since we’re making a linear dp vector of size n.