Table of Contents
Problem Statement
Range Sum Query 2D – Immutable Leetcode Solution – Given a 2D matrix matrix, handle multiple queries of the following type:
- Calculate the sum of the elements of
matrixinside the rectangle defined by its upper left corner(row1, col1)and lower right corner(row2, col2).
Implement the NumMatrix class:
NumMatrix(int[][] matrix)Initializes the object with the integer matrixmatrix.int sumRegion(int row1, int col1, int row2, int col2)Returns the sum of the elements ofmatrixinside the rectangle defined by its upper left corner(row1, col1)and lower right corner(row2, col2).
Example
Input
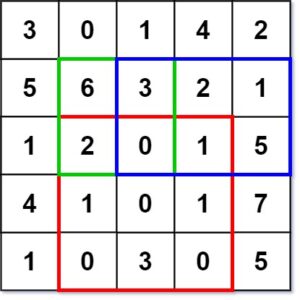
["NumMatrix", "sumRegion", "sumRegion", "sumRegion"] [[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
Output
[null, 8, 11, 12]
Explanation
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]); numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle) numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle) numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)
Constraints
m == matrix.lengthn == matrix[i].length1 <= m, n <= 200-105<= matrix[i][j] <= 1050 <= row1 <= row2 < m0 <= col1 <= col2 < n- At most
104 calls will be made tosumRegion.
Approach
Idea
The main idea here is to store the sum for each rectangle with its top-left on (0,0) and bottom-right on (i, j) where 1<=i<=m, 1<=j<=n.
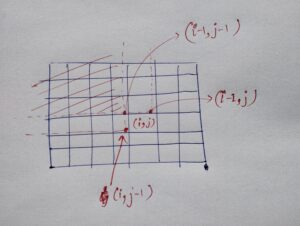
To calculate and store these sums in prefixSum matrix, we use the relation.prefixSum[i][j] = prefixSum[i-1][j] + prefixSum[i][j-1] - prefixSum[i-1][j-1] + mat[i-1][j-1];.As we are building upon the solution to the sub-problems, we are using the concept of Dynamic Programming here.
The image to imagine this relation is also attached.
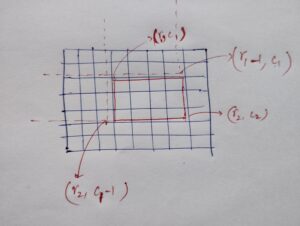
Then to query each sum in O(1) time we use the relation prefixSum[r2][c2] - prefixSum[r1-1][c2] - prefixSum[r2][c1-1] + prefixSum[r1-1][c1-1];As we are building upon the solution of the sub-problems, we are using the concept of Dynamic Programming here.
The image to imagine this relation is also attached.
Code
C++ Program of Range Sum Query 2D – Immutable
typedef vector<int> VI;
typedef vector<VI> VVI;
class NumMatrix {
private:
int prefixSum[200+3][200+3];
public:
NumMatrix(vector<vector<int>>& mat) {
int n = mat.size(), m = mat[0].size();
memset(prefixSum, 0, sizeof(prefixSum));
for(int i = 1;i<=n;i++){
for(int j = 1;j<=m;j++){
prefixSum[i][j] = prefixSum[i-1][j] + prefixSum[i][j-1] - prefixSum[i-1][j-1] + mat[i-1][j-1];
}
}
}
int sumRegion(int r1, int c1, int r2, int c2) {
r1++, c1++, c2++, r2++;
return prefixSum[r2][c2] - prefixSum[r1-1][c2] - prefixSum[r2][c1-1] + prefixSum[r1-1][c1-1];
}
};Java Program of Range Sum Query 2D – Immutable
class NumMatrix {
long[][] prefixSum;
public NumMatrix(int[][] mat) {
int n = mat.length, m = mat[0].length;
prefixSum = new long[n+1][m+1];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
prefixSum[i][j] = mat[i-1][j-1] + prefixSum[i-1][j] + prefixSum[i][j-1] - prefixSum[i-1][j-1];
}
public int sumRegion(int R1, int C1, int R2, int C2) {
R1+=1;C1+=1;R2+=1;C2+=1;
return (int)(prefixSum[R2][C2] - prefixSum[R2][C1-1] - prefixSum[R1-1][C2] + prefixSum[R1-1][C1-1]);
}
}Python3 Program of Range Sum Query 2D – Immutable
class NumMatrix:
def __init__(self, mat: List[List[int]]):
n, m = len(mat), len(mat[0])
self.prefixSum = [[0] * (m+1) for _ in range(n+1)]
for i in range(1, n+1):
for j in range(1, m+1):
self.prefixSum[i][j] = mat[i-1][j-1] + self.prefixSum[i-1][j] + self.prefixSum[i][j-1] - self.prefixSum[i-1][j-1]
def sumRegion(self, R1: int, C1: int, R2: int, C2: int) -> int:
return self.prefixSum[R2+1][C2+1] - self.prefixSum[R2+1][C1] - self.prefixSum[R1][C2+1] + self.prefixSum[R1][C1]Complexity Analysis for Range Sum Query 2D – Immutable Leetcode Solution
Time Complexity
O(1) per query.
O(m*n) to build the prefixSum 2D matrix.
Space Complexity
O(m*n) to store the prefixSum 2D matrix.