Same Tree LeetCode Solution

Difficulty Level Easy
Frequently asked in Adobe Amazon American Express Apple Bloomberg Facebook Google LinkedIn Microsoft OracleViews 5223

Problem Statement

The problem Same Tree says Given the roots of two binary trees p and q, write a function to check if they are the same or not.

Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.

Example:

Test Case 1:

Input:

p = [3, 9, 20, null, null, 15, 7]

q = [3, 9, 20, null, null, 15, 7]

Same Tree LeetCode Solution

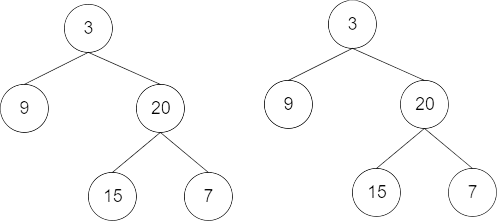
Output:

true

Test Case 2:

Input:

p = [10, 20]

q = [10, null, 20]

Output:

false

Explanation:

i) For the first test case, both the trees have the same structure and values. So the output is true.

ii) In the second test case, although both the trees have the same values but structure of both the trees is different. So the output is false.

Approach

Idea:

We can divide both the trees into smaller, smaller sub-trees recursively and check if they are the same. While dividing the trees, we can check if the left subtree of one parent tree is the same as the left subtree of the other parent tree. We can do the same for the right subtrees also. If all the subtrees are equal, the output will be true otherwise the output will be false.

Note: We might feel, if the traversal of both the trees is the same, the trees will be the same but for some trees (for ex: test case 2) the traversal value will be the same but the trees are not the same.

Code

Java Program for Same Tree LeetCode Solution

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p==null&&q==null)
          return true;
        if(p==null||q==null||p.val!=q.val)
          return false;
        return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
    }
}

C++ Program for Same Tree LeetCode Solution

class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(p==NULL&&q==NULL)
          return true;
        if(p==NULL||q==NULL||p->val!=q->val)
          return false;
        return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
    }
};

Complexity Analysis for Same Tree LeetCode Solution

Time Complexity

Here we visit each node exactly once. So time complexity is O(n), where n is the number of nodes in the tree.

Space Complexity

In the case of a balanced tree, the space complexity will be O(logn). In the case of an unbalanced tree, the space complexity will be O(n).

Reference: https://en.wikipedia.org/wiki/Binary_tree

 

 

 

 

 

Translate »