Table of Contents
Problem Statement
Search Suggestions System LeetCode Solution – You are given an array of strings products and a string searchWord.
Design a system that suggests at most three product names from products after each character of searchWord is typed. Suggested products should have a common prefix with searchWord. If there are more than three products with a common prefix return the three lexicographically minimums products.
Return a list of lists of the suggested products after each character of searchWord is typed.
Example
Test Case 1:
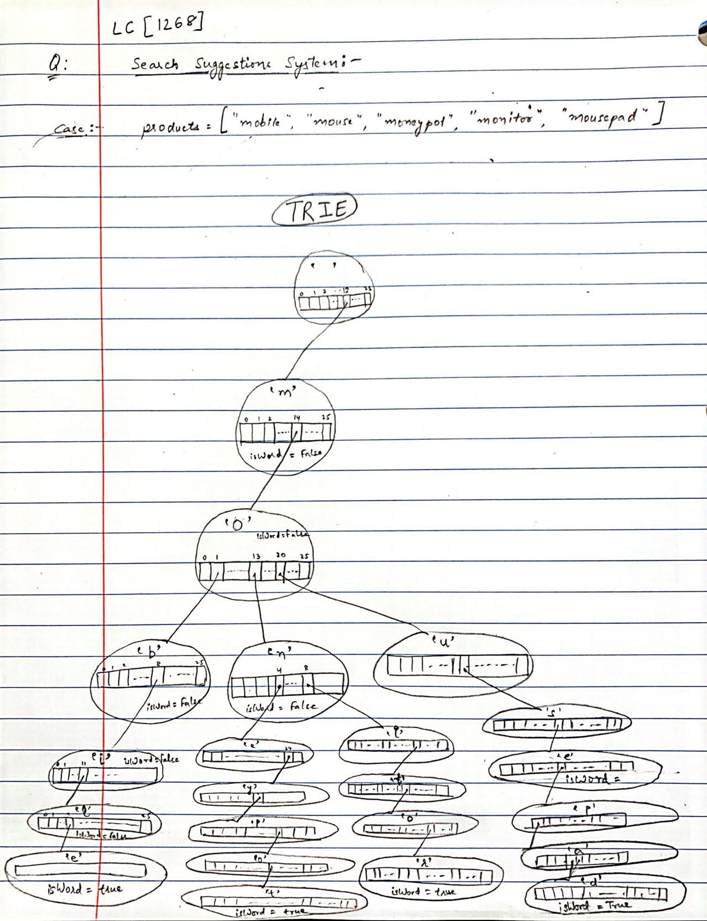
Input:
products = [“mobile”,”mouse”,”moneypot”,”monitor”,”mousepad”]
searchWord = “mouse”
Output:
[ [“mobile”,”moneypot”,”monitor”], [“mobile”,”moneypot”,”monitor”], [“mouse”,”mousepad”], [“mouse”,”mousepad”], [“mouse”,”mousepad”] ]
Explanation
products sorted lexicographically =[“mobile”,”moneypot”,”monitor”,”mouse”,”mousepad”].
After typing m and mo all products match and we show user [“mobile”,”moneypot”,”monitor”]
After typing mou, mous and mouse the system suggests [“mouse”,”mousepad”]
Approach:
TrieNode design
Now let us think about how we will process nodes in lexicographical order. At that stage, the crucial role in plays design of the TrieNode data structure.
First, we can save the order of child nodes by using an array with the same length as the English alphabet. However, the disadvantage of that solution is that we use a lot of redundant space because most of the array’s positions can be empty.
Second, we can use a hash table. That way we will get rid of the array redundancy. To explore the child nodes in lexicographical order we will have to iterate through the alphabet and check if a certain letter exists as a key in the dictionary. That way we will spend in a worst-case just O(26) time to check all possible keys.
In conclusion, we discussed two implementations of the TrieNode data structure and their trade-offs. The second solution uses much lesser space than the first one. But the time needed in the worst case remains the same O(26).
Prefix match queries
I think we a doing great so far. Now, let us go one step further. To find any number of words on each level of the prefix match we have to explore the tree where the current node of the Trie is the root. To do so we have to use a tree-traversal algorithm, such as DFS. In the worst case, a recursive DFS-call will take O(n * k * s) time and O(n) auxiliary space. That is a lot of work, isn’t it?
To save that time and space we can use an array node.ids to store indices of words from the original collection of words whose prefixes match the path to the current node in the Trie. That way to find words with a specific prefix takes constant time. All we have to do is to iterate through the node.ids array and return the corresponding values from the original collection.
Seems that this change saved us a lot of time and space. However, one more time by solving one problem we just created another. The order of words’ indices in node.ids array must represent the words in lexicographical order. To maintain the order we have to sort the initial collection words and add words into the Trie in that order.
Idea:
Idea is to iterate through the products and store the prefixes into a Trie.
Important Points:
- The Trie Node will hold at most 3 words, and those words will be the lexicographically minimum words. This is optimized for fast search word keystrokes results.
- A Heap will be used to ensure the 3 words that are stored in the Trie nodes will be the lexicographically minimum words.
- When all of the previous is completed, each search word keystroke will be an optimized O(1) constant operation.
Code for Search Suggestions System
Java Program
class Solution {
public List<List<String>> suggestedProducts(String[] products, String searchWord) {
Trie trie = new Trie();
for(String product : products){ // update trie data-structure with all products,
trie.insert(product); // by inserting each product to trie
}
return trie.search(trie, 3, searchWord, new ArrayList<List<String>>() ); // search in Trie, and keep updating final list
}
// ==================================================== Trie data-structure ====================================================== //
class Trie {
TrieNode root;
public Trie() { // Trie Constructor
root = new TrieNode(' '); // Create root node, with ' ' as val.
}
// -----------------------------------------------------------------
public List<List<String>> search(Trie trie, int count, String searchWord, List<List<String>> resultList){ // search in Trie, and keep updating final list
for(int i = 1; i <= searchWord.length(); i++){
List<String> list = new ArrayList<String>();
TrieNode node = trie.root;
String typedSoFar = searchWord.substring(0, i);
node = reachLastCharOfPrefix(typedSoFar, count, node ); // call method to first reach last node of current substring (prefix)
list = depthFirstSearch(node, list, count); // call *DFS* to search further on all chilren of node
resultList.add(list);
}
return resultList;
}
// -----------------------------------------------------------------
public List<String> depthFirstSearch(TrieNode node, List<String> list, int count){
if(node == null || list.size() >= count){ return list; } // if node is null, or, List got 3 strings by now, return list. Don't forget "node == null"
if(! node.word.isEmpty()){ list.add(node.word); } // if node's word is not Empty, we have found the word. add it to list, and continue further
for(TrieNode childNode : node.children){
if(childNode == null){ continue; }
list = depthFirstSearch(childNode, list, count); // call DFS/recursion on childNode
}
return list;
}
// -----------------------------------------------------------------
public TrieNode reachLastCharOfPrefix(String prefix, int count, TrieNode node) {
for(int i = 0; i < prefix.length(); i++){
char ch = prefix.charAt(i);
if(node.children[ch - 'a'] == null){ return null; }
node = node.children[ch - 'a'];
}
return node;
}
// -----------------------------------------------------------------
public void insert(String word) { // Let's we are inserting word "mobile"
TrieNode node = this.root;
for(int i = 0; i < word.length(); i++){ // loop through each char of word
char ch = word.charAt(i); // let's say first char is 'm' which is to be inserted
if(node.children[ch - 'a'] == null){ // if child exists at children[m - 'a']. children[109-97] = children[12]
node.children[ch - 'a'] = new TrieNode(ch); // then insert new TrieNode object of value 'm' at children[12]
}
node = node.children[ch - 'a']; // go to next child node
}
node.word = word;
}
// ========================= class TrieNode ======================== //
static class TrieNode{
char val; // node's char value e.g. 'm'
TrieNode[] children; // each node can have upto 26 children.
String word = "";
TrieNode(char val){ // pass val in the constructor
this.val = val;
children = new TrieNode[26]; // because every child is of char type. we have 26 characters.
}
}
}
}Python Program
from collections import defaultdict
from heapq import heappush, heappop
class MinWord:
def __init__(self, word):
self.word = word
# Update the comparator here so we are retaining the lexographically
# smaller words as the heap is a min_heap
def __lt__(self, other):
return self.word > other.word
class TrieNode:
def __init__(self):
self.children = defaultdict(TrieNode)
self.words = [] # Heap that will store at most 3 words
class Trie:
def __init__(self):
self.root = TrieNode()
# O(n) (n = length of the word) time complexity
def add_word(self, word):
n = self.root
for char in word:
n = n.children[char]
heappush(n.words, MinWord(word)) # TODO i mistakenly flipped these 2 vars
if len(n.words) > 3:
heappop(n.words)
class Solution:
# O(m*n + s) (m = length of the products, n = length of a word, s = length of search word) time complexity
def suggestedProducts(self, products: "List[str]", searchWord: str) -> "List[List[str]]":
trie = Trie()
suggestions = []
for product in products: # O(m*n) (m = length of the products) time complexity
trie.add_word(product) # O(n) (n = length of the word) time complexity
n = trie.root
for key in searchWord: # O(s) (s = length of the search word) time complexity
n = n.children[key]
suggestions.append(sorted([min_word.word for min_word in n.words]))
return suggestionsComplexity Analysis for Search Suggestions System LeetCode Solution
Time: O(m * n + s * k). To construct the Trie data structure we have to iterate throughout all words which takes time proportional to O(m * n). After creating the Trie we will iterate over all characters in searchWord and on each step, we will make at most k iterations to collect the matched words. In our case, the k = 3 and in terms of BigO notation can be dropped. But in a case where there are no limits or k is an argument, we will have to clearly specify it.
Space: O(26 ** n + s * k). Trie data structure takes at most O(26 ** n space because each node can have at most 26 child nodes. The depth of the Trie is the maximum length of the word. Also, we have to pay for extra O(s * k) space to store the result.