Smallest Range II Leetcode Solution

Difficulty Level Medium
Frequently asked in Adobe AppleViews 2340

Problem Statement :

Smallest Range II Leetcode Solution – You are given an integer array nums and an integer k.

For each index i where 0 <= i < nums.length, change nums[i] to be either nums[i] + k or nums[i] – k.

The score of nums is the difference between the maximum and minimum elements in nums.

Return the minimum score of nums after changing the values at each index.

Example :

Example 1 

Input: nums = [1], k = 0
Output: 0
Explanation: The score is max(nums) - min(nums) = 1 - 1 = 0.

Example 2

Input: nums = [0,10], k = 2
Output: 6
Explanation: Change nums to be [2, 8]. The score is max(nums) - min(nums) = 8 - 2 = 6.

Example 3

Input: nums = [1,3,6], k = 3
Output: 3
Explanation: Change nums to be [4, 6, 3]. The score is max(nums) - min(nums) = 6 - 3 = 3.

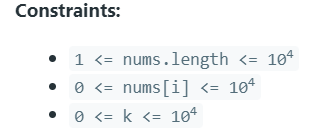
Constraints :

Smallest Range II Leetcode Solution

Observation :

  • Let the maximum element in the array be max and the minimum element is min.
  • If we were not allowed to change the array values then it is quite clear that the maximum difference (maxdiff) will be

                                                                         maxdiff= max-min.

    • But our goal is to minimize this difference, But in what way can we do that? Obviously by either increasing or decreasing the heights by k. Let’s try all the possible combinations of increasing and decreasing min and max.
  • Increasing both maximum and minimum heights :
    New maximum = max + k
    New minimum =  min + k
    New maxdiff = ( max + k ) – ( min + k ) = max – min
    This is the same as the original maxdiff. Hence increasing both the values don’t change the original answer and hence is of no use.
  • Decreasing both maximum and minimum heights :
    New maximum = max – k
    New minimum =min – k
    New maxdiff = ( max – k) – ( min – k) = max – min
    This is the same as the original maxdiff. Hence decreasing both the values don’t change the original answer and hence is of no use.
  • Increasing maximum and decreasing minimum heights :
    New maximum = max + k
    New minimum =  min – k
    New maxdiff = ( max + k ) – ( min – k) = max – min  + 2*k
    We increased our original difference by 2*k. This will worsen our answer and hence is of no use.
  • Decreasing maximum and Increasing minimum heights :
    New maximum = max –  k
    New minimum = min +  k
    New maxdiff = (  max –  k ) – ( min +  k ) = max-min  – 2*k
    We decreased our original difference by 2*k. This will improve our answer.

Hence we must decrease the maximum value of the array and increase the minimum value to improve our answer.

Algorithm :

  • Initially sort the array, so that we can find one of the best differences between the min value and max value in the given array. (i.e., ans variable in the above code).
  • Now, iterate in the array and increase the current i’th value by k and compare with nums[n-1]-k, to find the new max.
  • Decrease the i’th + 1  by k and find the new min by comparing nums[0]+k.
  •  Finally, return ans which stores the min diff of max-min.

Code for Smallest Range II

Java  Code

// we need to find min Score (Maximum - Minimum )
// for minmising we can decrease the maximum one or else we can increase the minimum
// first find the min and max of nums
class Solution {
    public int smallestRangeII(int[] nums, int k) {
 int n = nums.length;
        Arrays.sort(nums);
        int maxE=nums[n-1];
        int minE=nums[0];
        int ans=maxE-minE;

        for (int i = 0; i < n - 1; ++i) {
            
            int currMax = Math.max(nums[n-1] - k, nums[i] + k);
            int currMin = Math.min(nums[0] + k, nums[i+1] - k);
            ans = Math.min(ans, currMax - currMin);
        }
        return ans;
    }
}

C++  Code

class Solution {
public:
    int smallestRangeII(vector<int>& nums, int k) {
        int n=nums.size();
        sort(nums.begin(),nums.end());
        int maxE=nums[n-1];
        int minE=nums[0];
        int ans=maxE-minE;
        for(int i=0;i<n-1;i++){
            int currMax=max(maxE-k,nums[i]+k);
            int currMin=min(minE+k,nums[i+1]-k);
            ans=min(currMax-currMin,ans);
            
        }
        return ans;
        
    }
};

Complexity Analysis for  Smallest Range II Leetcode Solution

Time Complexity

, where N is the length of the nums.

Space Complexity 

 O(1).

Translate »