In the problem, “Special Array With X Elements Greater Than or Equal X”, we are given an array of non-negative integers. We need to find some integer X such that there are exactly X elements greater than or equal to it in the array. If there is no possible X that satisfies this condition, we need to output -1.
Table of Contents
Example
1 2 3 4
-1
1 3 4 5
3
Approach(Brute Force)
It is certain that if there exists a solution X, then X will always be unique.
Proof:
Consider there are two solutions X and Y such that X != Y. Lets assume X < Y. Now, number of elements greater than or equal to X should be X as we consider it as a solution. But, since Y > X, there are Y elements greater than or equal to X such that X != Y. Hence our assumption of X being a solution is wrong unless X and Y are equal.
So, there is always a unique solution, if a solution exists. Now, it can also be concluded that if X is a solution, then the number of elements greater than/equal to it = X, which should be less than N, where N = size of the array(as the maximum number of elements possible = N).
So, if a solution X exists, then it must lie in the range [1, N].
We can check for every integer in the range [1, N] if the number of elements in the array that are greater than or equal to any integer in the range is equal to that integer itself. For example, consider Array = {1 , 3 , 4 , 5}. Now, 1 and 2 have 4 and 3 elements greater than or equal to them in the array respectively. Number of elements greater than/equal to 3 = 3. So, 3 is the only solution. Since we traverse the whole tree to find the number of elements greater than for every integer in the range: [1, N], this approach is slow.
Algorithm
- Run a loop from i = 1 to i = N to check for solution:
- Count the number of elements greater than or equal to ‘i‘ in the array
- If the count is equal to ‘i‘, return i
- Count the number of elements greater than or equal to ‘i‘ in the array
- Return -1;
Implementation of Special Array With X Elements Greater Than or Equal X Leetcode Solution
C++ Program
#include <bits/stdc++.h>
using namespace std;
int specialArray(vector <int> &a)
{
int n = a.size() , counter = 0;
for(int i = 1 ; i <= n ; i++)
{
counter = 0;
for(int j = 0 ; j < n ; j++)
if(a[j] >= i)
counter++;
if(counter == i)
return i;
}
return -1;
}
int main()
{
vector <int> a = {1 , 3 , 4 , 5};
cout << specialArray(a) << '\n';
}
Java Program
class special_array
{
public static void main(String args[])
{
int[] a = {1 , 3 , 4 , 5};
System.out.println(specialArray(a));
}
static int specialArray(int[] a)
{
int n = a.length , counter = 0;
for(int i = 1 ; i <= n ; i++)
{
counter = 0;
for(int j = 0 ; j < n ; j++)
if(a[j] >= i)
counter++;
if(counter == i)
return i;
}
return -1;
}
}
3
Complexity Analysis of Special Array With X Elements Greater Than or Equal X Leetcode Solution
Time Complexity
O(N * N), N = Size of the array. In the worst case, when X = N is the solution, we make O(N * N) comparisons.
Space complexity
O(1). Only constant memory space is used.
Approach(Optimal)
We can store the number of occurrences of all elements in a table, using an array. Note that for any element with a value greater than N, we can count it as an occurrence of an element with value N because the maximum value of the solution can be N.
Now, the frequency of elements greater than or equal to X = frequency of X + frequency of all elements greater than X. In order to find this for every element in the range [1, N], we need to have a suffix frequency array.
So, for every integer in the array, we need to set frequency[i] = frequency[i] + frequency[i + 1], for every ‘i‘ in range [N – 1 , 1], which will create a suffix frequency array, storing number of elements greater than or equal to ‘i‘ as frequency[i].
Now, because of the lookup table, we can check a solution for any integer in the range [1, N] in O(1) time. This is a case where we trade off memory to improve on time. Since the table is of size N, we have no worries of memory limits as well.
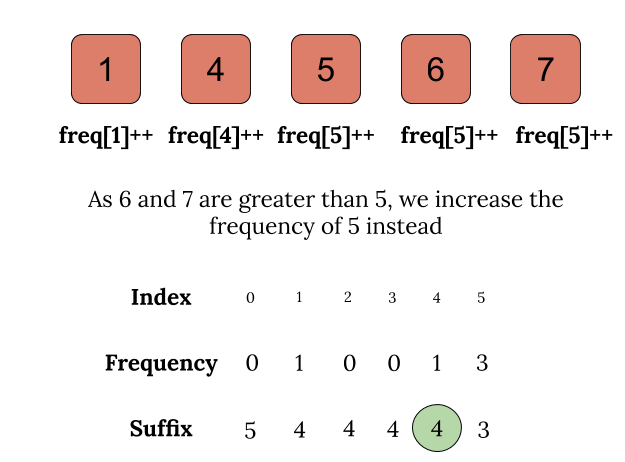
Algorithm
- Initialize a frequency array of size N, having each value as zero
- For every element i in the array:
- If i > N, increment frequency[N]
- Increment frequency[i]
- Create a suffix sum array from frequency as:
- For every element ranging from i = N – 1 to i = 0
- set frequency[i] = frequency[i] + frequency[i + 1]
- For every element ranging from i = N – 1 to i = 0
- Run a loop from i = 1 to i = N
- If i == frequency[i], return i
- return -1
Implementation of Special Array With X Elements Greater Than or Equal X Leetcode Solution
C++ Program
#include <bits/stdc++.h>
using namespace std;
int specialArray(vector<int>& a)
{
int n = a.size();
vector <int> frequency(n + 1 , 0);
for(int i = 0 ; i < n ; i++)
if(a[i] > n)
frequency[n]++;
else
frequency[a[i]]++;
for(int i = n - 1 ; i >= 0 ; i--)
frequency[i] += frequency[i + 1];
for(int i = 0 ; i <= n ; i++)
if(frequency[i] == i)
return i;
return -1;
}
int main()
{
vector <int> a = {1 , 3 , 4 , 5};
cout << specialArray(a) << '\n';
}
Java Program
class special_array
{
public static void main(String args[])
{
int[] a = {1 , 3 , 4 , 5};
System.out.println(specialArray(a));
}
static int specialArray(int[] a)
{
int n = a.length;
int[] frequency = new int[n + 1];
for(int i = 0 ; i < n ; i++)
frequency[i] = 0;
for(int i = 0 ; i < n ; i++)
if(a[i] > n)
frequency[n]++;
else
frequency[a[i]]++;
for(int i = n - 1 ; i >= 0 ; i--)
frequency[i] += frequency[i + 1];
for(int i = 0 ; i <= n ; i++)
if(frequency[i] == i)
return i;
return -1;
}
}
3
Complexity Analysis of Special Array With X Elements Greater Than or Equal X Leetcode Solution
Time Complexity
O(N), N = Size of the array. We can check for any integer in O(1) time, so in the worst case, we use O(N) time.
Space complexity
O(N). Linear memory space is used for storing frequencies.