Table of Contents
Problem Statement
In Special Positions in a Binary Matrix problem a matrix of size n*m is given in which there are only two type of values 1s and 0s. A cell position is called special if value of that cell is 1 and values in all the cells in that particular row and column is 0. We have to return how many special positions are there in the matrix.
Example
mat = [[1,0,0],
[0,0,1],
[1,0,0]]1
Explanation: (1,2) is a special position because mat[1][2] == 1 and all other elements in row 1 and column 2 are 0.
mat = [[1,0,0],
[0,1,0],
[0,0,1]]3
Explanation: (0,0), (1,1) and (2,2) are special positions.
Brute Force Approach
To solve the above problem we can apply brute force solution. i.e. We can go to each cell (i,j) and if its value is 1 then there is a chance of this cell to be special. So for this particular cell(i,j) we would traverse row(i) and col(j) completely and count how many 1s are there in that row and that column. If there is only one 1s in this row as well as only one 1s in this column then this cell is counted as special cell. Example of 4*4 matrix:
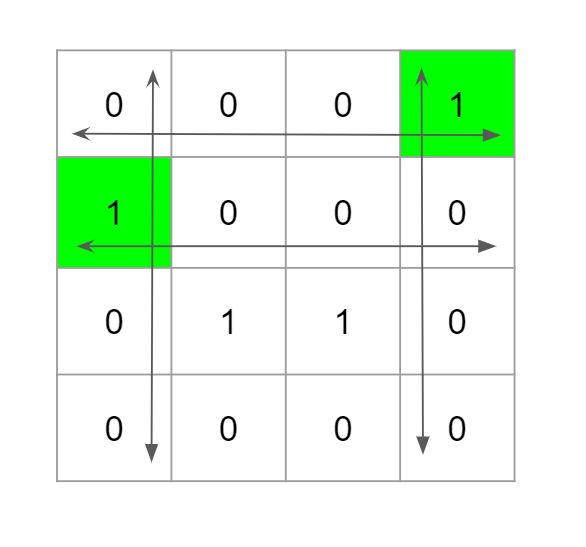
Algorithm
Create a variable special to count the special positions.
Traverse the matrix using nested loop for cell(i,j).
If value of current cell(i,j) is 1, then:
Traverse the row(i) and find the count of 1s in that row.
Traverse the col(j) and find the count of 1s in that column.
if count of 1s in row(i) is 1 and count of 1s in col(j) is also 1, then:
Increment the count of special position.
Return the value of variable special.Implementation for Special Positions in a Binary Matrix Leetcode Solution
C++ Program
#include <bits/stdc++.h>
using namespace std;
int numSpecial(vector<vector<int>>& mat)
{
int n=mat.size();
int m=mat[0].size();
int special=0;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
if(mat[i][j])
{
int col=0,row=0;
for(int k=0;k<n;k++) col+= mat[k][j];
for(int k=0;k<m;k++) row+= mat[i][k];
if(col==1 && row==1) special++;
}
return special;
}
int main()
{
vector<vector<int> > mat={
{0,0,0,1},
{1,0,0,0},
{0,1,1,0},
{0,0,0,0}
};
cout<<numSpecial(mat)<<endl;
return 0;
}2
Java Program
import java.lang.*;
class Rextester
{
public static int numSpecial(int[][] mat)
{
int n=mat.length;
int m=mat[0].length;
int special=0;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
if(mat[i][j]==1)
{
int col=0,row=0;
for(int k=0;k<n;k++) col+= mat[k][j];
for(int k=0;k<m;k++) row+= mat[i][k];
if(col==1 && row==1) special++;
}
return special;
}
public static void main(String args[])
{
int[][] mat={
{0,0,0,1},
{1,0,0,0},
{0,1,1,0},
{0,0,0,0}
};
System.out.println(numSpecial(mat));
}
}2
Complexity Analysis for Special Positions in a Binary Matrix Leetcode Solution
Time Complexity
O(n*m*(n+m)) : In worst case we are traversing a row and a column i.e. O(n+m) for each cell in the matrix. Hence Time complexity will be O(n*m*(n+m)).
Space Complexity
O(1) : We are not using any extra memory here.
Optimised Approach
We can optimise the above approach by reducing the linear work for each cell to a constant time by doing some pre-processing.
What can we do is, initially we can store the count of 1s for each row and each column in a two linear arrays. Then we traverse each cell and check if its value is 1, then we check if count of 1s in this row and this column is also equal to one or not using count arrays. This checking for a particular row and column, we can do now in constant time. That’s the benefit of using some extra memory, it can reduce time complexity. An example of 4*4 matrix is shown in fig below:
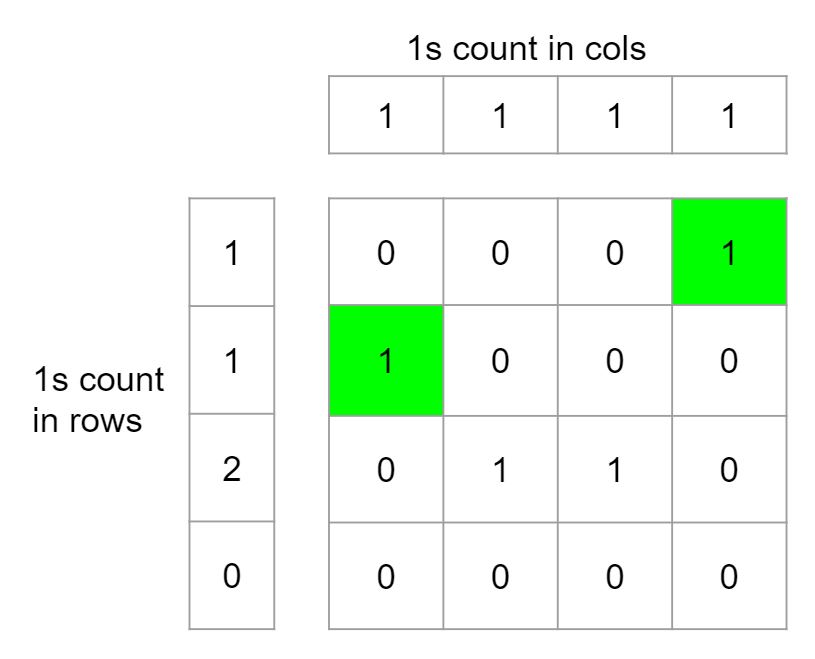
Algorithm :
Create a variable special to count the special positions.
Create two arrays rows and cols of size n and m respectively.
Traverse each row(i) and count the numbers of 1s for each row and store it in rows[i].
Traverse each col(i) and count the numbers of 1s for each column and store it in cols[i].
Traverse the matrix using nested loop for cell (i,j).
If value of current cell(i,j) is 1 and rows[i]==1 and cols[j]==1, then:
Increment the count of special position.
Return the value of variable special.Implementation for Special Positions in a Binary Matrix Leetcode Solution
C++ Program
#include <bits/stdc++.h>
using namespace std;
int numSpecial(vector<vector<int>>& mat)
{
int n=mat.size();
int m=mat[0].size();
int special=0;
int* rows= new int[n];
int* cols= new int[m];
for(int i=0;i<n;i++)
{
int cnt=0;
for(int j=0;j<m;j++) cnt+=mat[i][j];
rows[i]=cnt;
}
for(int j=0;j<m;j++)
{
int cnt=0;
for(int i=0;i<n;i++) cnt+=mat[i][j];
cols[j]=cnt;
}
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
if( mat[i][j]==1 && rows[i]==1 && cols[j]==1 ) special++;
return special;
}
int main()
{
vector<vector<int> > mat={
{0,0,0,1},
{1,0,0,0},
{0,1,1,0},
{0,0,0,0}
};
cout<<numSpecial(mat)<<endl;
return 0;
}2
Java Program
import java.lang.*;
class Rextester
{
public static int numSpecial(int[][] mat)
{
int n=mat.length;
int m=mat[0].length;
int special=0;
int[] rows= new int[n];
int[] cols= new int[m];
for(int i=0;i<n;i++)
{
int cnt=0;
for(int j=0;j<m;j++) cnt+=mat[i][j];
rows[i]=cnt;
}
for(int j=0;j<m;j++)
{
int cnt=0;
for(int i=0;i<n;i++) cnt+=mat[i][j];
cols[j]=cnt;
}
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
if( mat[i][j]==1 && rows[i]==1 && cols[j]==1 ) special++;
return special;
}
public static void main(String args[])
{
int[][] mat={
{0,0,0,1},
{1,0,0,0},
{0,1,1,0},
{0,0,0,0}
};
System.out.println(numSpecial(mat));
}
}2
Complexity Analysis for Special Positions in a Binary Matrix Leetcode Solution
Time Complexity
O(n*m) : Here we are running two nested loops for finding number of 1s. i.e. O(2*n*m). Then we traversed each cell of the matrix which take O(n*m). Therefore overall time complexity will be O(n*m).
Space Complexity
O(n+m) : We have used two linear arrays of size n and m. Therefore space complexity will be O(n+m).