Spiral Matrix III LeetCode Solution

Difficulty Level Medium
Frequently asked in Facebook TeslaViews 3358

Problem Statement

Spiral Matrix III LeetCode Solution – You start at the cell (rStart, cStart) of an rows x cols grid facing east. The northwest corner is at the first row and column in the grid, and the southeast corner is at the last row and column.

You will walk in a clockwise spiral shape to visit every position in this grid. Whenever you move outside the grid’s boundary, we continue our walk outside the grid (but may return to the grid boundary later.). Eventually, we reach all rows * cols spaces of the grid.

Return an array of coordinates representing the positions of the grid in the order you visited them.

Example:

Input:

rows = 5,

cols = 6,

rStart = 1,

cStart = 4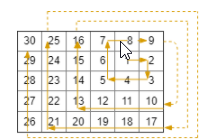Spiral Matrix III LeetCode Solution

Output: 

[[1,4], [1,5], [2,5], [2,4], [2,3], [1,3], [0,3], [0,4], [0,5], [3,5], [3,4 ], [3,3], [3,2], [2,2], [1,2], [0,2], [4,5], [4,4], [4,3], [4,2], [4,1], [3,1], [2,1], [1,1], [0,1], [4,0], [3,0], [2,0], [1,0], [0,0]]

Explanation for Spiral Matrix III LeetCode Solution:

Intuition:

Take steps one by one.
If the location is inside of the grid, add it to res.
But how to simulate the path?

It seems to be annoying, but if we observe the path:

move right 1 step, turn right
move down 1 step, turn right
move left 2 steps, turn right
move top 2 steps, turn right,
move right 3 steps, turn right
move down 3 steps, turn right
move left 4 steps, turn right
move top 4 steps, turn right,

we can find the sequence of steps: 1,1,2,2,3,3,4,4,5,5….

So there are two things to figure out:

  1. how to generate sequence 1,1,2,2,3,3,4,4,5,5
  2. how to turn right?Spiral Matrix III LeetCode Solution
  • Starting with a step length of 1, move one time to the right, then turn; move one time to below
  • Increase step length, 1 + 1 = 2, move 2 times to left, then turn; move 2 times to above
  • So, for each step length, we will move step for 2 directions, then increase step by one; and repeat
  • To summarize:
    • Step == 1, move*step, turn, move*step, turn
    • Step += 1, move*step, turn, move*step, turn
    • Step += 1, move*step, turn, move*step, turn
    • ... ... repeat

Code for Spiral Matrix III LeetCode Solution

Java Program

class Solution {
    public int[][] spiralMatrixIII(int R, int C, int x, int y) {
        int[][] res = new int[R * C][2];
        int dx = 0, dy = 1, n = 0, tmp;
        for (int j = 0; j < R * C; ++n) {
            for (int i = 0; i < n / 2 + 1; ++i) {
                if (0 <= x && x < R && 0 <= y && y < C)
                    res[j++] = new int[] {x, y};
                x += dx;
                y += dy;
            }
            tmp = dx;
            dx = dy;
            dy = -tmp;
        }
        return res;
    }
}

C++ Program

class Solution {
public:
    vector<vector<int>> spiralMatrixIII(int R, int C, int r, int c) {
        vector<vector<int>> res = {{r, c}};
        int dx = 0, dy = 1, tmp;
        for (int n = 0; res.size() < R * C; n++) {
            for (int i = 0; i < n / 2 + 1; i++) {
                r += dx, c += dy;
                if (0 <= r && r < R && 0 <= c && c < C)
                    res.push_back({r, c});
            }
            tmp = dx, dx = dy, dy = -tmp;
        }
        return res;
    }
};

Python Program

class Solution(object):
    def spiralMatrixIII(self, R, C, x, y):
        res = []
        dx, dy, n = 0, 1, 0
        while len(res) < R * C:
            for i in xrange(n / 2 + 1):
                if 0 <= x < R and 0 <= y < C:
                    res.append([x, y])
                x, y = x + dx, y + dy
            dx, dy, n = dy, -dx, n + 1
        return res

Complexity Analysis for Spiral Matrix III LeetCode Solution

Time Complexity: O(max(R,C)^2)
Space  Complexity: O(R*C) for output

Translate »