Table of Contents
Problem Statement
The Maze III LeetCode Solution – There is a ball in a maze with empty spaces (represented as 0) and walls (represented as 1). The ball can go through the empty spaces by rolling up, down, left or right, but it won’t stop rolling until hitting a wall. When the ball stops, it could choose the next direction. There is also a hole in this maze. The ball will drop into the hole if it rolls onto the hole.
Given the m x n maze, the ball’s position ball and the hole’s position hole, where ball = [ballrow, ballcol] and hole = [holerow, holecol], return a string instructions of all the instructions that the ball should follow to drop in the hole with the shortest distance possible. If there are multiple valid instructions, return the lexicographically minimum one. If the ball can’t drop in the hole, return "impossible".
If there is a way for the ball to drop in the hole, the answer instructions should contain the characters 'u' (i.e., up), 'd' (i.e., down), 'l' (i.e., left), and 'r' (i.e., right).
The distance is the number of empty spaces traveled by the ball from the start position (excluded) to the destination (included).
You may assume that the borders of the maze are all walls (see examples).
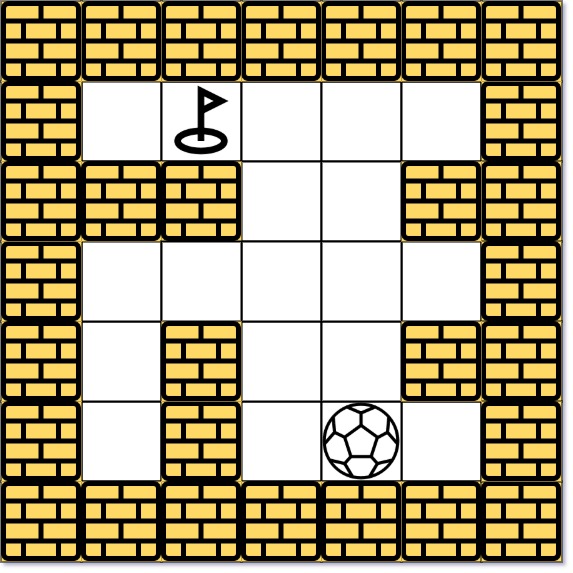
Input: maze = [[0,0,0,0,0],[1,1,0,0,1],[0,0,0,0,0],[0,1,0,0,1],[0,1,0,0,0]], ball = [4,3], hole = [0,1] Output: "lul" Explanation: There are two shortest ways for the ball to drop into the hole. The first way is left -> up -> left, represented by "lul". The second way is up -> left, represented by 'ul'. Both ways have shortest distance 6, but the first way is lexicographically smaller because 'l' < 'u'. So the output is "lul".
Explanation
Each time, first add the direction to the path, and then go with that direction, checking for holes along the way. When hitting a wall, try to turn, and go in a new direction. For the starting point, don’t “go”, jump directly to the “turn” part.
We aim to find the path passing the shortest distance. So objects in the BFS queue should be PathElements, i.e., cells in the maze.
We restrict the order of orientations during initialization to ensure the final answer is lexicographically smallest.
For each cell, it can at most be visited 4 times for there are 4 orientations. So boolean[][][] visited is three-dimensional.
The start PathElement should be any one of the 4 cells around the ball if the cell is valid. So we add the 4 start PathElements first.
During BFS, we move on following the original orientation. If we can’t go forward anymore (i.e., meet the edge or wall), we turn to the other 3 orientations. We keep track of the orientation and path on the fly, whenever we meet the hole, we return the current path, that’s also why we set attributes orientation and move to class PathElement.
Code
C++ Code for The Maze III
class Solution {
public:
string roll(vector<vector<int>>& maze, int rowBall, int colBall, const vector<int>& hole,
int d_row, int d_col, int steps, const string& path, pair<string, int>& res)
{
if (steps < res.second) {
if (d_row != 0 || d_col != 0) { // both are zero for the initial ball position.
while ((rowBall + d_row) >= 0 && (colBall + d_col) >= 0 && (rowBall + d_row) < maze.size()
&& (colBall + d_col) < maze[0].size() && maze[rowBall + d_row][colBall + d_col] != 1)
{
rowBall += d_row;
colBall += d_col;
++steps;
if (rowBall == hole[0] && colBall == hole[1] && steps < res.second) res = {path, steps};
}
}
if (maze[rowBall][colBall] == 0 || steps + 2 < maze[rowBall][colBall]) {
maze[rowBall][colBall] = steps + 2; // '1' is for the walls.
if (d_row == 0) roll(maze, rowBall, colBall, hole, 1, 0, steps, path + "d", res);
if (d_col == 0) roll(maze, rowBall, colBall, hole, 0, -1, steps, path + "l", res);
if (d_col == 0) roll(maze, rowBall, colBall, hole, 0, 1, steps, path + "r", res);
if (d_row == 0) roll(maze, rowBall, colBall, hole, -1, 0, steps, path + "u", res);
}
}
return res.first;
}
string findShortestWay(vector<vector<int>>& maze, vector<int>& ball, vector<int>& hole)
{
return roll(maze, ball[0], ball[1], hole, 0, 0, 0, "", pair<string, int>() = {"impossible", INT_MAX});
}
};Java Code for The Maze III
public class Solution {
int min; //min distance to hole
String minS; //min distance's path string
int[] hole;
int[][] maze;
int[][] map; //shortest distant traveling from ball to this point
int[][] dirs = {{0,1},{-1,0},{1,0},{0,-1}}; //r, u, d, l
public String findShortestWay(int[][] maze, int[] ball, int[] hole) {
this.min = Integer.MAX_VALUE;
this.minS = null;
this.hole = hole;
this.maze = maze;
this.map = new int[maze.length][maze[0].length];
for(int i = 0; i<map.length; i++) Arrays.fill(map[i], Integer.MAX_VALUE);
move(ball[0], ball[1], 0, "", -1);
return (minS==null) ? "impossible" : minS;
}
private void move(int r, int c, int cnt, String path, int dir){//dir is a index of dirs
if(cnt > min || cnt > map[r][c]) return; //not a shortest route for sure
if(dir!=-1){//if not from start point
//add path
if(dir==0) path+='r';
else if(dir==1) path+='u';
else if(dir==2) path+='d';
else path+='l';
//roll along dir
while(r>=0 && r<maze.length && c>=0 && c<maze[0].length && maze[r][c]==0){
map[r][c] = Math.min(map[r][c], cnt);
if(r==hole[0] && c==hole[1]){//check hole
if(cnt==min && path.compareTo(minS)<0){
minS=path;
}else if(cnt<min){
min = cnt;
minS = path;
}
return;
}
r += dirs[dir][0];
c += dirs[dir][1];
cnt++;
}
r -= dirs[dir][0];//[r,c] is wall, need to walk back 1 step
c -= dirs[dir][1];
cnt--;
}
//hit wall (or start) -> try to turn
for(int i = 0; i<dirs.length; i++){
if(dir == i) continue;//dont keep going
if(dir == (3-i)) continue;//dont go back
int newR = r + dirs[i][0];
int newC = c + dirs[i][1];
if(newR>=0 && newR<maze.length && newC>=0 && newC<maze[0].length && maze[newR][newC]==0){//can go
move(r, c, cnt, path, i);
}
}
}
}Python Code for The Maze III
class Solution:
def findShortestWay(self, maze, ball, hole):
m, n, q, stopped = len(maze), len(maze[0]), [(0, "", ball[0], ball[1])], {(ball[0], ball[1]): [0, ""]}
while q:
dist, pattern, x, y = heapq.heappop(q)
if [x, y] == hole:
return pattern
for i, j, p in ((-1, 0, "u"), (1, 0, "d"), (0, -1, "l"), (0, 1, "r")):
newX, newY, d = x, y, 0
while 0 <= newX + i < m and 0 <= newY + j < n and maze[newX + i][newY + j] != 1:
newX += i
newY += j
d += 1
if [newX, newY] == hole:
break
if (newX, newY) not in stopped or [dist + d, pattern + p] < stopped[(newX, newY)]:
stopped[(newX, newY)] = [dist + d, pattern + p]
heapq.heappush(q, (dist + d, pattern + p, newX, newY))
return "impossible"Complexity Analysis for The Maze III LeetCode Solution
Time Complexity
O(V+E)
Space Complexity
O(V)