Sum Root to Leaf Numbers LeetCode Solution

Difficulty Level Medium
Frequently asked in Adobe Amazon Apple Bloomberg Facebook Google Microsoft Paytm
Binary Tree Depth First Search TreeViews 2514

Problem Statement

Sum Root to Leaf Numbers LeetCode Solution says – You are given the root of a binary tree containing digits from 0 to 9 only.

Each root-to-leaf path in the tree represents a number.

  • For example, the root-to-leaf path 1 -> 2 -> 3 represents the number 123.

Return the total sum of all root-to-leaf numbers. Test cases are generated so that the answer will fit in a 32-bit integer.

A leaf node is a node with no children.

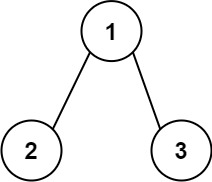
Sum Root to Leaf Numbers LeetCode Solution

Input: root = [1,2,3]
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.

Sum Root to Leaf Numbers LeetCode Solution

Input: root = [4,9,0,5,1]
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.

Explanation

We recursively go to each node and check if it is null or not
a- If it is a null node, then we skip it and move to the next
b- If it is not a null node, we multiply the current by 10, and add the node value

We repeat the same procedure for all the nodes present, to get the final answer and return it.

Code

Java Solution:

class Solution {
    
    public int sumNumbers(TreeNode root) {
        
        return solve(root, 0);
    }
    
    int solve(TreeNode root, int curr){
        
        if(root == null){
            return 0;
        }
        
        curr = curr*10 + root.val;
        
        if(root.left == null && root.right == null){
            //leaf node
            return curr ;
        }
        
        return solve(root.left, curr) + solve(root.right, curr);
    }
}

 

C++ Solution

class Solution {
public:
    
    void solve(TreeNode* root, int ans, int &fans)
    {
        if(!root)
            return;
        
        if(!root->left && !root->right)
        {
            ans = ans *10 + root->val;
            fans +=ans;
            return;
        }
        
        ans = ans *10 + root->val;
        solve(root->left, ans, fans);
        solve(root->right, ans,fans);
    }
    int sumNumbers(TreeNode* root) 
    {
        int ans =0;
        int fans = 0;
        solve(root, ans, fans);
        return fans;
    }
};

Complexity Analysis of Sum Root to Leaf Numbers Leetcode Solution:

Time complexity O(N) where N is number of Nodes

Space complexity O(H) where H is the height of the tree

Translate »