Valid Perfect Square LeetCode Solution

Difficulty Level Easy
Frequently asked in Adobe Amazon Facebook Google LinkedIn MicrosoftViews 2118

Problem Statement

Valid Perfect Square LeetCode Solution – Given a positive integer num, write a function that returns True if num is a perfect square else False.

Follow up: Do not use any built-in library function such as sqrt.

Input: num = 16
Output: true

Explanation

A boundary for our solution is fixed. for any number n, it’s square-root can lie between 1 and n so we know that the answer will be in 1 to n.

Simple Approach

Check for every number in 1 to n. would take O(n) time.

Optimized Approach

The idea is simple we just find all pair divisors. We iterate from 2 to …, and when we find a divisor,
we try to divide num by it one more time.

For example:
input: num = 180

iterate beginning from 2:
180%2==0 ?
yes -> num = 180/2 = 90

check if we can divide by 2 again:
90%2==0 ?
yes -> num = 90/2 = 45

num is 45 now.
since num was decreased, we should again iterate beginning from 2:

45%2==0 ?
no -> continue to iterate

45%3==0 ?
yes -> nums = 45/3 = 15
let’s divide one more time

15%3==0 ?
yes -> nums = 15/3 = 5
num is 5 now.

num was decreased -> again iterate beginning from 2
5%2==0 ?
no -> continue to iterate
5%3==0 ?
no -> continue to iterate
5%4==0 ?
no -> continue to iterate
5%5==0 ?
yes -> nums = 5/5 = 1
check if we can divide one more time:
1%5==0 ?
no -> return false

Apply binary search on the search space and the problem can be solved in O(log n) time.

Valid Perfect Square LeetCode Solution

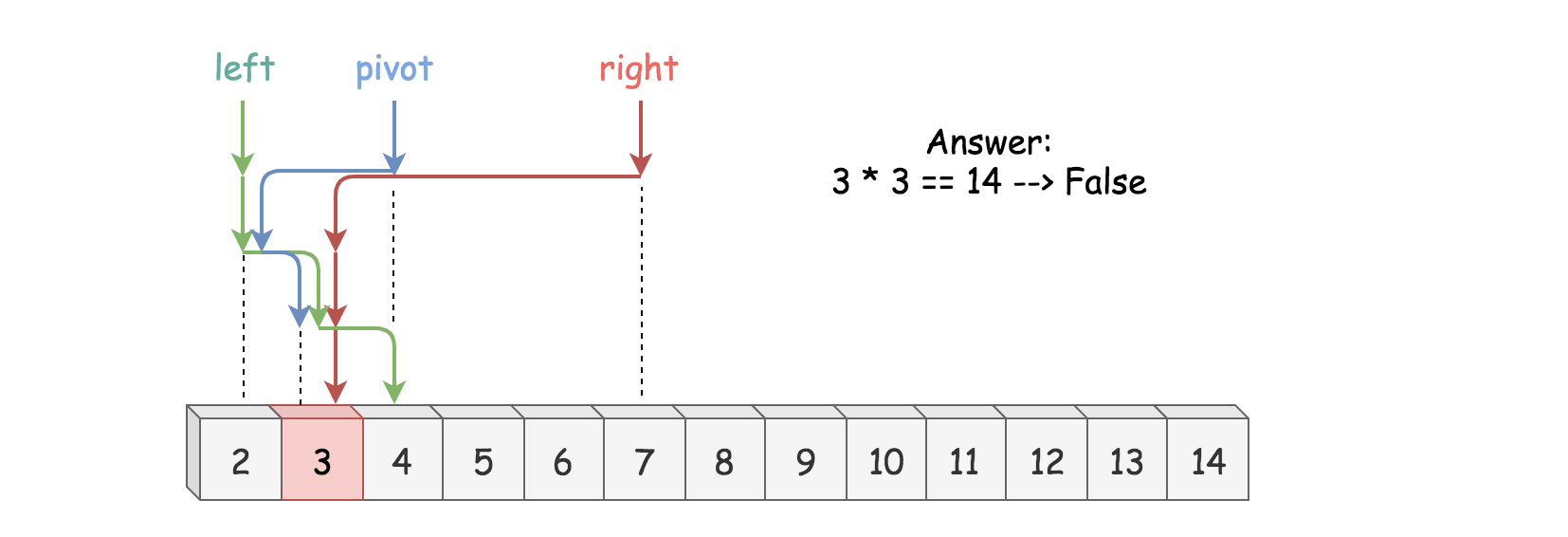
Code

C++ Code For  Valid Perfect Square

class Solution {
public:
    bool isPerfectSquare(int num) {
        if (num < 0) return false;
        if (num == 0 || num == 1) return true;
        
        int i = 0;
        int j = num;
        
        while (i <= j) {
            long b = i + (j-i)/2;
            
            if (b*b == num)
                return true;
            else if (b*b < num)
                i = b+1;
            else
                j = b-1;
        }
        
        return false;
    }
};

Java Code For  Valid Perfect Square

class Solution {
    public boolean isPerfectSquare(int num) {
        int low=1, high=num;
        while(low<=high) {
            long mid=(low+high)>>>1;
            if(mid*mid==num) return true;
            else if(mid*mid>num) high=(int)mid-1;
            else low=(int)mid+1;
        }
        return false;
    }
}

Python Code For  Valid Perfect Square

class Solution:
    def isPerfectSquare(self, num: int) -> bool:
        left = 0
        right = num
        while left <= right:

            mid = (left+right)//2

            if mid*mid==num:
                return True
            elif mid*mid > num:
                right = mid - 1
            else:
                left = mid+1
        return False

Complexity Analysis for Valid Perfect Square LeetCode Solution

Time Complexity

Time Complexity of binary search is: O(log n)

Space Complexity

Space Complexity of binary search is: O(1)

Reference: https://en.wikipedia.org/wiki/Perfect_square

Translate »