Valid Perfect Square Leetcode Solution

Difficulty Level Easy
Frequently asked in Amazon
algorithms coding Interview interviewprep LeetCode LeetCodeSolutionsViews 5433

This post is on Valid Perfect Square Leetcode Solution

Problem statement

In the problem “Valid Perfect Square” we are given a number “num” and we need to check if this number is a perfect square or not. We have to check this without using the built-in sqrt function.

If the number is a perfect square then we will return true else we will return false.

Example

num = 25
true

Explanation:

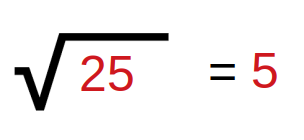
Valid Perfect Square Leetcode Solution

25 is a valid perfect square as its square root is 5. So, the answer becomes true.

Approach

As we can’t use built-in functions so, the basic approach to solve this problem is to check each number from 1 to num and find its square then check if its square is equal to num. If the square is equal to num then num is a Valid Perfect Square so, we will return true else we will return false.

In spite of linearly checking each number, we can improve the solution by using a binary search approach. In this approach, we need to decide our search range , start point, and endpoint.

  1. The start point will be 1.
  2. The endpoint will be num because the square of any number greater than num will be always greater than num.
  3. So the range for then binary search is 1 to num.
  4. Now we will find the square of mid. If the square is equal to num then we will return true else:
    1. if the square is greater than num then our endpoint will reduce to mid-1.
    2. else start point will become mid+1.
  5. In the end, if num does not match with any square of number then we will return false.

Code

C++ code for Valid Perfect Square Leetcode Solution

#include <bits/stdc++.h> 
using namespace std; 
    bool isPerfectSquare(int num) {
        int s=1,e=num;
        while(s<=e)
        {
            long long int mid=s+(e-s)/2;
            if(mid*mid==num)
                return true;
            else if(mid*mid>num)
             e=mid-1;
            else
                s=mid+1;
        }
        return false;
    }
int main() 
{ 
 int num=25;
 cout<<boolalpha;
 cout<<isPerfectSquare(num)<<endl; 
 return 0;
}
true

Java code for Valid Perfect Square Leetcode Solution

import java.util.Arrays; 
public class Tutorialcup {
    public static  boolean isPerfectSquare(int num){
    long s=1,e=num;
        while(s<=e)
        {
            long mid=s+(e-s)/2;
            if(mid*mid==num)
                return true;
            else if(mid*mid>num)
             e=mid-1;
            else
                s=mid+1;
        }
        return false;
    }
  public static void main(String[] args) {
    int num=25;
    boolean ans=  isPerfectSquare(num);
    System.out.println(ans);
  }
}
true

Complexity Analysis of Valid Perfect Square Leetcode Solution

Time complexity

The time complexity of the above code is O(logn). Here n is the value of num.

Space complexity

The space complexity of the above code is O(1) because we are using only a variable to store answer.

References

Translate ยป