Valid Tic-Tac-Toe State LeetCode Solution

Difficulty Level Medium
Frequently asked in Amazon Apple Bloomberg Facebook Google Microsoft OracleViews 1943

Problem Statement

Valid Tic-Tac-Toe State LeetCode Solution – We are given a Tic-Tac-Toe board as a string array board & are asked to return true iff it is possible to reach this board position during the course of a valid tic-tac-toe game. The board is a 3 x 3 array that consists of characters ‘ ‘, ‘X’, & ‘O’. The ‘ ‘ character represents an empty square.

Rules of Tic-Tac-Toe:

  • Players take turns placing characters into empty squares ‘  ‘.
  • The first player always places ‘X’ characters, while the second player always places ‘O’ characters.
  •  ‘X’  and ‘O’  characters are always placed into empty squares, never filled ones.
  • The game ends when there are three of the same (non-empty) character filling any row, column, or diagonal.
  • The game also ends if all squares are non-empty.
  • No more moves can be played if the game is over.

Constraints:

  • board.length == 3
  • board[i].length == 3
  • board[i][j] is either ‘X’ , ‘O’, or  ‘  ‘

Examples & Explanations

Example 1:

Valid Tic-Tac-Toe State LeetCode Solution

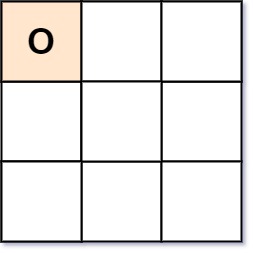
Input: board = ["O  ","   ","   "]
Output: false
Explanation: The first player always plays "X".

Example 2:

Valid Tic-Tac-Toe State LeetCode Solution

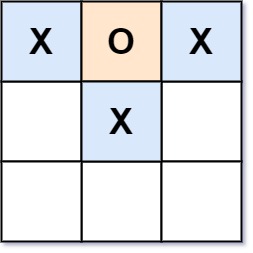
Input: board = ["XOX"," X ","   "]
Output: false
Explanation: Players take turns making moves.

Example 3:

Valid Tic-Tac-Toe State LeetCode Solution

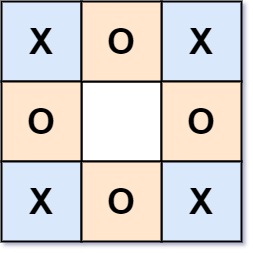
Input: board = ["XOX","O O","XOX"]
Output: true
Explanation: This state of game is achievable.

Approach

The approach discussed here is brute force, it is easy to implement if edge cases are begin taken care of. Let’s call player marking X, playerX and player marking O, playerO. We know that playerX wins if 3 X’s are marked on the board either row-wise or col-wise or diagonal-wise or anti-diagonal-wise, & similarly with playerO.

We will use variables rows & cols of size 3 to keep the count of X’s and O’s. For every X marked in row i and column j, we will increment the value of rows[i] and cols[j] by 1and for every O marked, we will decrement the value by 1. Use another variable diag and antiDiag to keep track of diagonal & anti-diagonal marked char. Increment by 1 diag if X is marked and decrement by 1 otherwise.

To know if players have played their turns at their chances, keep a variable turn, which increases by 1 when X is marked and decreases by 1 otherwise. Since playerX starts the game, the value of turn can be 0 or 1.

Then we will check all the necessary conditions like –

  • only one player can win
  • turn == 0 or 1, if not return false
  • playerX wins but turn ≠ 1 ⇒ not possible
  • playerO wins but turn ≠ 0 ⇒ not possible

Code

C++ code for Valid Tic-Tac-Toe State

class Solution {
public:
    bool validTicTacToe(vector<string>& board) {
        int rows[3]={0,0,0}, cols[3]={0,0,0}, diag=0, antiDiag=0, turns=0;

        for(int i=0; i<3; i++) {
            for(int j=0; j<3; j++) {
                if(board[i][j] == 'X') {
                    rows[i]++;
                    cols[j]++;
                    if(i==j) diag++;
                    if(i+j == 2) antiDiag++;
                    turns++;
                }
                else if(board[i][j] == 'O') {
                    rows[i]--;
                    cols[j]--;
                    if(i==j) diag--;
                    if(i+j == 2) {
                        antiDiag--;
                    }
                    turns--;
                }
                
            }
        }
        
        bool Xwins = rows[0] == 3 || rows[1] == 3 || rows[2] == 3 || 
                cols[0] == 3 || cols[1] == 3 || cols[2] == 3 || 
                diag == 3 || antiDiag == 3;
        bool Owins = rows[0] == -3 || rows[1] == -3 || rows[2] == -3 || 
                cols[0] == -3 || cols[1] == -3 || cols[2] == -3 || 
                diag == -3 || antiDiag == -3;
        
        
        if ((Xwins && turns != 1) || (Owins && turns != 0)) return 0;
        if(Xwins && Owins) return 0;
        return (turns == 0 || turns == 1);
        
        
    }
};

Java code for Valid Tic-Tac-Toe State

class Solution {
    public boolean validTicTacToe(String[] board) {
        int turns = 0;
        int[] rows = new int[3];
        int[] cols = new int[3];
        int diag = 0;
        int antiDiag = 0;
        
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 3; j++) {
                if (board[i].charAt(j) == 'X') {
                    turns++; 
                    rows[i]++; 
                    cols[j]++;
                    if (i == j) diag++;
                    if (i + j == 2) antiDiag++;
                } else if (board[i].charAt(j) == 'O') {
                    turns--; 
                    rows[i]--; 
                    cols[j]--;
                    if (i == j) diag--;
                    if (i + j == 2) antiDiag--;
                }
            }
        }
        
    boolean Xwins = false;
        Xwins = rows[0] == 3 || rows[1] == 3 || rows[2] == 3 || 
               cols[0] == 3 || cols[1] == 3 || cols[2] == 3 || 
               diag == 3 || antiDiag == 3;
        
        boolean Owins = false;
        Owins = rows[0] == -3 || rows[1] == -3 || rows[2] == -3 || 
               cols[0] == -3 || cols[1] == -3 || cols[2] == -3 || 
               diag == -3 || antiDiag == -3;
        
        if ((Xwins && turns != 1) || (Owins && turns != 0)) return false;
        if(Xwins && Owins) return false;
        return (turns == 0 || turns == 1);
    }
}

Complexity Analysis for Valid Tic-Tac-Toe State LeetCode Solution

Translate »