Binary Tree Longest Consecutive Sequence LeetCode Solution

Difficulty Level Medium
Frequently asked in Amazon ByteDance Facebook Google PinterestViews 2062

Problem Statement

Binary Tree Longest Consecutive Sequence LeetCode Solution – Given the root of a binary tree, return the length of the longest consecutive sequence path.

The path refers to any sequence of nodes from some starting node to any node in the tree along with the parent-child connections. The longest consecutive path needs to be from parent to child (cannot be the reverse).

Binary Tree Longest Consecutive Sequence LeetCode Solution

 

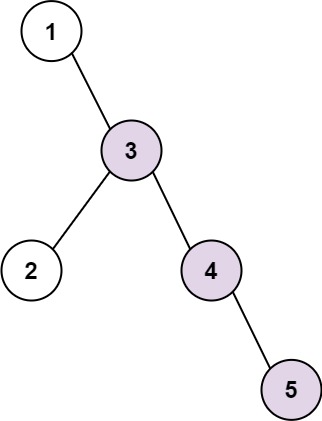
Input: root = [1,null,3,2,4,null,null,null,5]
Output: 3
Explanation:

Longest consecutive

 sequence path is 3-4-5, so return 3.

Explanation For Binary Tree Longest Consecutive Sequence

Just very intuitive depth-first search, send cur node value to the next level and compare it with the next level node.

Code for Binary Tree Longest Consecutive Sequence LeetCode Solution

C++ Code

class Solution {
public:
    int longestConsecutive(TreeNode* root) {
        return search(root, nullptr, 0);
    }
    
    int search(TreeNode *root, TreeNode *parent, int len) {
        if (!root) return len;
        len = (parent && root->val == parent->val + 1)?len+1:1;
        return max(len, max(search(root->left, root, len), search(root->right, root, len)));
    }
};

Java Code

public class Solution {
    private int max = 0;
    public int longestConsecutive(TreeNode root) {
        if(root == null) return 0;
        helper(root, 0, root.val);
        return max;
    }
    
    public void helper(TreeNode root, int cur, int target){
        if(root == null) return;
        if(root.val == target) cur++;
        else cur = 1;
        max = Math.max(cur, max);
        helper(root.left, cur, root.val + 1);
        helper(root.right, cur, root.val + 1);
    }
}

Python Code

class Solution:
     def longestConsecutive(self, root: TreeNode) -> int:
        def longest_path(root):
            if not root:
                return 0
            length = 1
            l = longest_path(root.left)
            r = longest_path(root.right)
            if root.left and root.left.val == root.val + 1:
                length = max(length, 1 + l)
            if root.right and root.right.val == root.val + 1:
                length = max(length, 1 + r)
            res[0] = max(res[0], length)
            return length
        
        res = [0]
        longest_path(root)
        return res[0]

Complexity Analysis For Binary Tree Longest Consecutive Sequence

Time Complexity: O(n) DFS traversal of a binary tree with n nodes takes O(n) time.

Space Complexity: O(1) no extra space is used.

Reference: https://en.wikipedia.org/wiki/Depth-first_search

Translate »