Table of Contents
Problem Statement
Path With Maximum Minimum Value LeetCode Solution – Given an m x n integer matrix grid, return the maximum score of a path starting at (0, 0) and ending at (m - 1, n - 1) moving in the 4 cardinal directions.
The score of a path is the minimum value in that path.
- For example, the score of the path
8 → 4 → 5 → 9is4
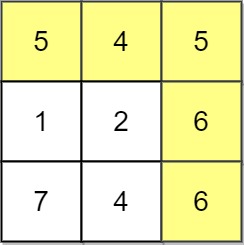
Input: grid = [[5,4,5],[1,2,6],[7,4,6]] Output: 4 Explanation: The path with the
is highlighted in yellow.
Explanation
Intuition:
- remove all the cells with value >=
min(begin,end) - sort all remaining unique values
- enumerate all remaining values to find a maximum value that is the minimum value in a path from the begin to the end; for each value, we use DFS to check whether there exists a path from begin to end such that this value is the minimum among the values in that path.
- if we find that value, we keep Binary Search to try to find a bigger value
- we lose our search criteria and see if there is a path from begin to end that all the values in that path >= a smaller value by moving the right pointer to the left
Why use DFS?
we use DFS to check if there exists a path from the being to the end
Why use Binary Search?
we use binary search to find the upper boundary. So when we find a valid value, we move the left pointer to mid + 1 to keep finding a larger value. Just as what we did in finding the first bad version: if we find a bad version, we move the right pointer to the mid – 1 to find an earlier bad product.
What is in the sorted array? / What are we binary search for?
Since we don’t know to whether a value ‘val’. in this sorted array is the minimum, so we deliberately make it be, by only considering the cells with values that are larger than this value. And if this arrangement doesn’t work (we cannot construct a path from begin to the end with ‘val’ being the minimum value seen) when BinarySearch(‘val’) returns False.
Code
C++ Code For Path With Maximum Minimum Value
class Solution {
public:
int maximumMinimumPath(vector<vector<int>>& A) {
static constexpr int DIRS[][2] {{0,1},{1,0},{0,-1},{-1,0}};
priority_queue<tuple<int,int,int>> pq;
pq.emplace(A[0][0], 0, 0);
int n = A.size(), m = A[0].size(), maxscore = A[0][0];
A[0][0] = -1; // visited
while(!pq.empty()) {
auto [a, i, j] = pq.top();
pq.pop();
maxscore = min(maxscore, a);
if(i == n - 1 && j == m - 1)
break;
for(const auto& d : DIRS)
if(int newi = d[0] + i, newj = d[1] + j;
newi >= 0 && newi < n && newj >= 0 && newj < m && A[newi][newj]>=0){
pq.emplace(A[newi][newj], newi, newj);
A[newi][newj] = -1;
}
}
return maxscore;
}
};Java Code For Path With Maximum Minimum Value
class Solution {
public int maximumMinimumPath(int[][] A) {
final int[][] DIRS = {{0,1},{1,0},{0,-1},{-1,0}};
Queue<int[]> pq = new PriorityQueue<>((a, b) -> Integer.compare(b[0], a[0]));
pq.offer(new int[] {A[0][0], 0, 0});
int maxscore = A[0][0];
A[0][0] = -1; // visited
while(!pq.isEmpty()) {
int[] top = pq.poll();
int i = top[1], j = top[2], n = A.length, m = A[0].length;
maxscore = Math.min(maxscore, top[0]);
if(i == n - 1 && j == m - 1)
break;
for(int[] d : DIRS) {
int newi = d[0] + i, newj = d[1] + j;
if(newi >= 0 && newi < n && newj >= 0 && newj < m && A[newi][newj]>=0){
pq.offer(new int[] {A[newi][newj], newi, newj});
A[newi][newj] = -1;
}
}
}
return maxscore;
}
}Python Code For Path With Maximum Minimum Value
class Solution:
def maximumMinimumPath(self, A: List[List[int]]) -> int:
dire = [(0, 1), (1, 0), (0, -1), (-1, 0)]
R, C = len(A), len(A[0])
maxHeap = [(-A[0][0], 0, 0)]
seen = [[0 for _ in range(C)] for _ in range(R)]
while maxHeap:
val, x, y = heapq.heappop(maxHeap)
# seen[x][y] = 1 # got TLE
if x == R - 1 and y == C - 1: return -val
for dx, dy in dire:
nx, ny = x + dx, y + dy
if 0 <= nx < R and 0 <= ny < C and not seen[nx][ny]:
seen[nx][ny] = 1 # passed
heapq.heappush(maxHeap, (max(val, -A[nx][ny]), nx, ny))
return -1Complexity Analysis for Path With Maximum Minimum Value LeetCode Solution
Time Complexity
- Time: O(MN log MN)
Space Complexity
- Space: O(MN)