Table of Contents
Problem Statement
Detect Squares LeetCode Solution – You are given a stream of points on the X-Y plane. Design an algorithm that:
- Adds new points from the stream into a data structure. Duplicate points are allowed and should be treated as different points.
- Given a query point, counts the number of ways to choose three points from the data structure such that the three points and the query point form an axis-aligned square with a positive area.
An axis-aligned square is a square whose edges are all the same length and are either parallel or perpendicular to the x-axis and y-axis.
Implement the DetectSquares class:
DetectSquares()Initializes the object with an empty data structure.void add(int[] point)Adds a new pointpoint = [x, y]to the data structure.int count(int[] point)Counts the number of ways to form axis-aligned squares with pointspoint = [x, y]as described above.
Example 1:
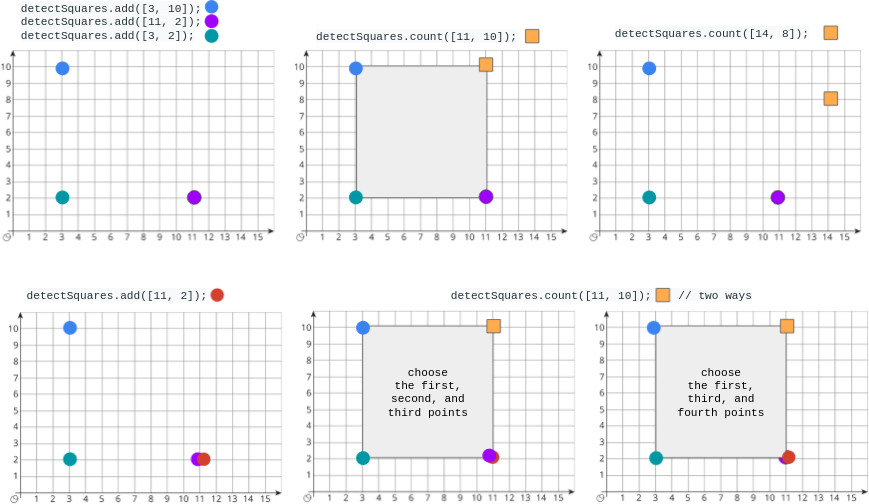 Input
Input
["DetectSquares", "add", "add", "add", "count", "count", "add", "count"] [[], [[3, 10]], [[11, 2]], [[3, 2]], [[11, 10]], [[14, 8]], [[11, 2]], [[11, 10]]]
Output
[null, null, null, null, 1, 0, null, 2]
Explanation
DetectSquares detectSquares = new DetectSquares();
detectSquares.add([3, 10]);
detectSquares.add([11, 2]);
detectSquares.add([3, 2]);
detectSquares.count([11, 10]); // return 1. You can choose:
// - The first, second, and third points
detectSquares.count([14, 8]); // return 0. The query point cannot form a square with any points in the data structure.
detectSquares.add([11, 2]); // Adding duplicate points is allowed.
detectSquares.count([11, 10]); // return 2. You can choose:
// - The first, second, and third points
// - The first, third, and fourth points
Constraints:
point.length == 20 <= x, y <= 1000- At most
3000calls in total will be made toaddandcount.
Approach
Idea:
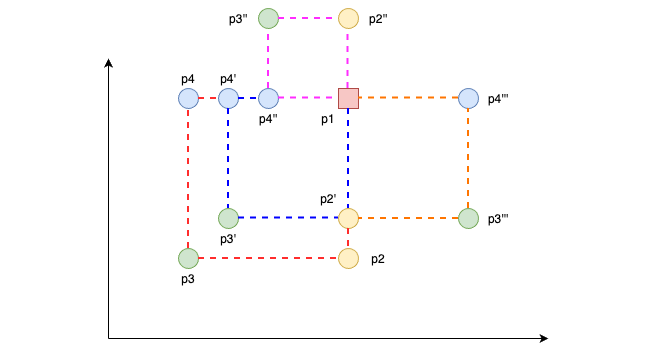
Given p1, try all points p3 (p1 and p3 form diagonal)
- To compute
count(p1):- First, We try all points
p3which together withp1,form the diagonal of the non-empty square. This meansabs(p1.x-p3.x) == abs(p1.y-p3.y) && abs(p1.x-p3.x) > 0 - Secondly, Since we have 2 points
p1andp3, we can form a square by computing the positions of the 2 remaining pointsp2,p4. - Thirdly, because of the above
p2 = (p1.x, p3.y) - Lastly, because of the above
p4 = (p3.x, p1.y)
- First, We try all points
Credit: https://assets.leetcode.com/users/images/3f33581d-baa5-4fd4-9516a1098af539d1_1632034530.1139376.png
Code
C++ Program of Detect Squares
class DetectSquares {
public:
int cntPoints[1001][1001] = {};
vector<pair<int, int>> points;
void add(vector<int> p) {
cntPoints[p[0]][p[1]]++;
points.emplace_back(p[0], p[1]);
}
int count(vector<int> p1) {
int x1 = p1[0], y1 = p1[1], ans = 0;
for (auto& [x3, y3] : points) {
if (abs(x1-x3) == 0 || abs(x1-x3) != abs(y1-y3))
continue;
ans += cntPoints[x1][y3] * cntPoints[x3][y1];
}
return ans;
}
};Java Program of Detect Squares
class DetectSquares {
int[][] cntPoints = new int[1001][1001];
List<int[]> points = new ArrayList<>();
public void add(int[] p) {
cntPoints[p[0]][p[1]] += 1;
points.add(p);
}
public int count(int[] p1) {
int x1 = p1[0], y1 = p1[1], ans = 0;
for (int[] p3 : points) {
int x3 = p3[0], y3 = p3[1];
if (Math.abs(x1-x3) == 0 || Math.abs(x1-x3) != Math.abs(y1-y3))
continue;
ans += cntPoints[x1][y3] * cntPoints[x3][y1];
}
return ans;
}
}Python Program of Detect Squares
class DetectSquares:
def __init__(self):
self.cntPoints = Counter()
def add(self, point: List[int]) -> None:
self.cntPoints[tuple(point)] += 1
def count(self, point: List[int]) -> int:
ans = 0
x1, y1 = point
for (x3, y3), cnt in self.cntPoints.items():
if abs(x1 - x3) == 0 or abs(x1 - x3) != abs(y1 - y3):
continue
ans += cnt * self.cntPoints[(x1, y3)] * self.cntPoints[(x3, y1)]
return ansComplexity Analysis for Detect Squares LeetCode Solution
Time Complexity
To begin with, the time complexity of the above code is O(1) because no matter how large our input is, we are still going to be running the same functions the same amount of times
Space Complexity
To end, the space complexity of the above code is O(1) because since we are doing only the same functions a constant amount of times, the space will also always be constant