Max Sum of Two Non-Overlapping Subarrays LeetCode Solution

Problem Statement

Max Sum of Two Non-Overlapping Subarrays LeetCode Solution – When given an integer array nums and two integers firstLen and secondLen, we return the maximum sum of elements in two non-overlapping subarrays with lengths firstLen and secondLen.

Also, the array with length firstLen could occur before or after the array with length secondLen, but they have to be non-overlapping.

A subarray is a contiguous part of an array.

This image shows this:

Max Sum of Two Non-Overlapping Subarrays LeetCode Solution

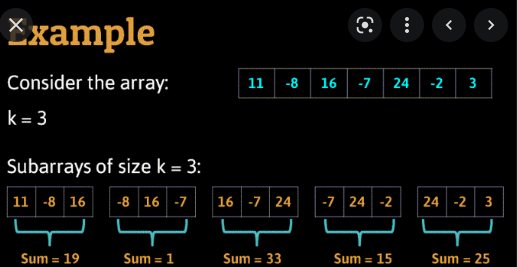
Credit: https://www.ideserve.co.in/learn/img/MaximumAverageSubarraySizeK.gif

Example 1:

Input:

 nums = [0,6,5,2,2,5,1,9,4], firstLen = 1, secondLen = 2

Output:

 20

Explanation:

 One choice of subarrays is [9] with length 1, and [6,5] with length 2.

Example 2:

Input:

 nums = [3,8,1,3,2,1,8,9,0], firstLen = 3, secondLen = 2

Output:

 29

Explanation:

 One choice of subarrays is [3,8,1] with length 3, and [8,9] with length 2.

Example 3:

Input:

 nums = [2,1,5,6,0,9,5,0,3,8], firstLen = 4, secondLen = 3

Output:

 31

Explanation:

 One choice of subarrays is [5,6,0,9] with length 4, and [0,3,8] with length 3.

Approach

Idea:

The main idea is that we want to both make the subarrays non-overlapping and secondly we want to make it so that we are adding the 2 subarrays with the largest totals so that our output is the largest that it can be. To go at this, firstly, we’ll calculate the prefix array sum. Now we tackle the other part of this problem which is making sure the subarrays are non-overlapping. Then, we’ll calculate the LMax value by considering L at leftmost, M at rightmost, and in the next pass, vice versa. And to reiterate, by keeping L and M at the ends of the array, we make the subarrays non-overlapping.

Code

Java Program of Maximum Sum of Two Non-Overlapping Subarrays:

class Solution {
     public int maxSumTwoNoOverlap(int[] A, int L, int M) {
        int sums[] = new int[A.length+1];
        int maxLval = 0;
        int maxRval = 0;
        int result = 0;
        
        for(int i=1;i<=A.length;i++)
            sums[i] = A[i-1]+sums[i-1];
        
        for(int i=L;i<=A.length-M;i++)
        {
            int currLVal = sums[i]-sums[i-L];
            int currMVal = sums[i+M]-sums[i];
            maxLval = Math.max(maxLval,currLVal);
            result = Math.max(result,currMVal+maxLval);
        }

        for(int i=M;i<=A.length-L;i++)
        {
            int currMVal = sums[i]-sums[i-M];
            int currLVal = sums[i+L]-sums[i];
            maxRval = Math.max(maxRval,currMVal);
            result = Math.max(result,currLVal+maxRval);
        }
        return result;
    }
}

C++ Program of Maximum Sum of Two Non-Overlapping Subarrays:

class Solution
{
    public:
    int maxSumTwoNoOverlap(std::vector<int> &A, int L, int M)
    {
        std::vector<int> sums(A.size() + 1);
        int maxLval = 0;
        int maxRval = 0;
        int result = 0;
        for (int i = 1; i <= A.size(); i++)
        {
            sums[i] = A[i - 1] + sums[i - 1];
        }
        for (int i = L; i <= A.size() - M; i++)
        {
            int currLVal = sums[i] - sums[i - L];
            int currMVal = sums[i + M] - sums[i];
            maxLval = max(maxLval,currLVal);
            result = max(result,currMVal + maxLval);
        }
        for (int i = M; i <= A.size() - L; i++)
        {
            int currMVal = sums[i] - sums[i - M];
            int currLVal = sums[i + L] - sums[i];
            maxRval = max(maxRval,currMVal);
            result = max(result,currLVal + maxRval);
        }
        return result;
    }
};

Python Program of Maximum Sum of Two Non-Overlapping Subarrays:

import math


class Solution :
    def  maxSumTwoNoOverlap(self, A,  L,  M) :
        sums = [0] * (len(A) + 1)
        maxLval = 0
        maxRval = 0
        result = 0
        i = 1
        while (i <= len(A)) :
            sums[i] = A[i - 1] + sums[i - 1]
            i += 1
        i = L
        while (i <= len(A) - M) :
            currLVal = sums[i] - sums[i - L]
            currMVal = sums[i + M] - sums[i]
            maxLval = max(maxLval,currLVal)
            result = max(result,currMVal + maxLval)
            i += 1
        i = M
        while (i <= len(A) - L) :
            currMVal = sums[i] - sums[i - M]
            currLVal = sums[i + L] - sums[i]
            maxRval = max(maxRval,currMVal)
            result = max(result,currLVal + maxRval)
            i += 1
        return result

Complexity Analysis for Max Sum of Two Non-Overlapping Subarrays LeetCode Solution

Time Complexity

Firstly, the time complexity of the above code is O(n) because we are traversing the array only once.

Space Complexity

Lastly, the space complexity of the above code is O(n) because we are using arrays to store and work with everything.

Translate »