Detect Squares LeetCode Solution

Problem Statement

Detect Squares LeetCode Solution – You are given a stream of points on the X-Y plane. Design an algorithm that:

  • Adds new points from the stream into a data structure. Duplicate points are allowed and should be treated as different points.
  • Given a query point, counts the number of ways to choose three points from the data structure such that the three points and the query point form an axis-aligned square with a positive area.

An axis-aligned square is a square whose edges are all the same length and are either parallel or perpendicular to the x-axis and y-axis.

Implement the DetectSquares class:

  • DetectSquares() Initializes the object with an empty data structure.
  • void add(int[] point) Adds a new point point = [x, y] to the data structure.
  • int count(int[] point) Counts the number of ways to form axis-aligned squares with points point = [x, y] as described above.

 

Example 1:

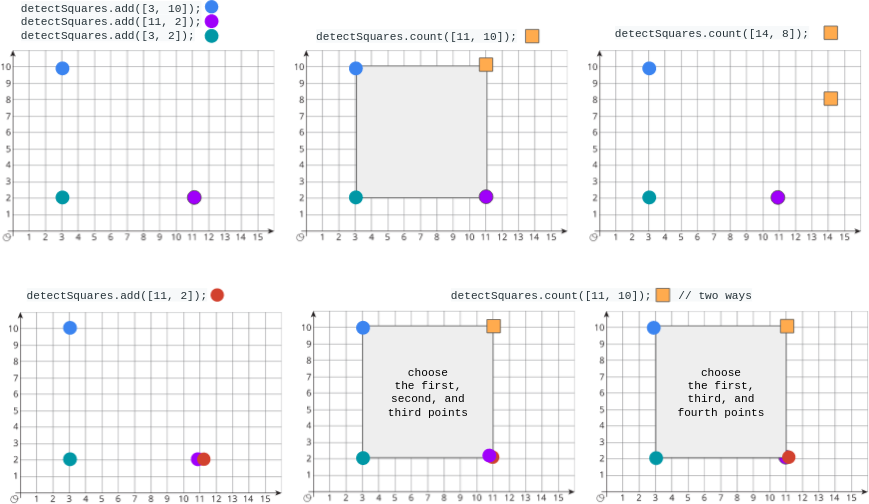Detect Squares LeetCode SolutionInput

["DetectSquares", "add", "add", "add", "count", "count", "add", "count"]
[[], [[3, 10]], [[11, 2]], [[3, 2]], [[11, 10]], [[14, 8]], [[11, 2]], [[11, 10]]]

Output

[null, null, null, null, 1, 0, null, 2]

Explanation

DetectSquares detectSquares = new DetectSquares();
detectSquares.add([3, 10]);
detectSquares.add([11, 2]);
detectSquares.add([3, 2]);
detectSquares.count([11, 10]); // return 1. You can choose:
                               //   - The first, second, and third points
detectSquares.count([14, 8]);  // return 0. The query point cannot form a square with any points in the data structure.
detectSquares.add([11, 2]);    // Adding duplicate points is allowed.
detectSquares.count([11, 10]); // return 2. You can choose:
                               //   - The first, second, and third points
                               //   - The first, third, and fourth points

 

Constraints:

  • point.length == 2
  • 0 <= x, y <= 1000
  • At most 3000 calls in total will be made to add and count.

Approach

Idea:

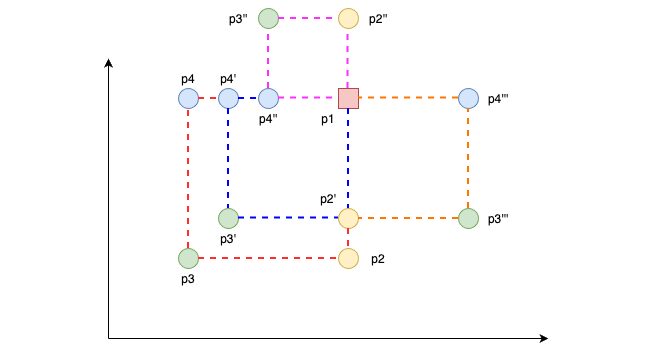
 Given p1, try all points p3 (p1 and p3 form diagonal)

  • To compute count(p1):
    • First, We try all points p3 which together with p1, form the diagonal of the non-empty square. This means abs(p1.x-p3.x) == abs(p1.y-p3.y) && abs(p1.x-p3.x) > 0
    • Secondly, Since we have 2 points p1 and p3, we can form a square by computing the positions of the 2 remaining points p2, p4.
    • Thirdly, because of the abovep2 = (p1.x, p3.y)
    • Lastly, because of the abovep4 = (p3.x, p1.y)

Detect Squares LeetCode Solution

Credit: https://assets.leetcode.com/users/images/3f33581d-baa5-4fd4-9516a1098af539d1_1632034530.1139376.png

Code

C++ Program of Detect Squares

class DetectSquares { 
public:
    int cntPoints[1001][1001] = {};
    vector<pair<int, int>> points;

    void add(vector<int> p) {
        cntPoints[p[0]][p[1]]++;
        points.emplace_back(p[0], p[1]);
    }

    int count(vector<int> p1) {
        int x1 = p1[0], y1 = p1[1], ans = 0;
        for (auto& [x3, y3] : points) {
            if (abs(x1-x3) == 0 || abs(x1-x3) != abs(y1-y3))
                continue;
            ans += cntPoints[x1][y3] * cntPoints[x3][y1];
        }
        return ans;
    }
};

Java Program of Detect Squares

class DetectSquares { 
    int[][] cntPoints = new int[1001][1001];
    List<int[]> points = new ArrayList<>();

    public void add(int[] p) {
        cntPoints[p[0]][p[1]] += 1;
        points.add(p);
    }

    public int count(int[] p1) {
        int x1 = p1[0], y1 = p1[1], ans = 0;
        for (int[] p3 : points) {
            int x3 = p3[0], y3 = p3[1];
            if (Math.abs(x1-x3) == 0 || Math.abs(x1-x3) != Math.abs(y1-y3))
                continue; 
            ans += cntPoints[x1][y3] * cntPoints[x3][y1];
        }
        return ans;
    }
}

Python Program of Detect Squares

class DetectSquares:
    def __init__(self):
        self.cntPoints = Counter()

    def add(self, point: List[int]) -> None:
        self.cntPoints[tuple(point)] += 1

    def count(self, point: List[int]) -> int:
        ans = 0
        x1, y1 = point
        for (x3, y3), cnt in self.cntPoints.items():
            if abs(x1 - x3) == 0 or abs(x1 - x3) != abs(y1 - y3):
                continue 
            ans += cnt * self.cntPoints[(x1, y3)] * self.cntPoints[(x3, y1)]
        return ans

Complexity Analysis for Detect Squares LeetCode Solution

Time Complexity

To begin with, the time complexity of the above code is O(1) because no matter how large our input is, we are still going to be running the same functions the same amount of times

Space Complexity

To end, the space complexity of the above code is O(1) because since we are doing only the same functions a constant amount of times, the space will also always be constant

Translate »