In the Minimum Height Trees problem, we have given an undirected graph which is tree in nature (acyclic and fully connected graph). Find out those vertices (or vertex) in the graph that when taken as root, will give tree with minimum height.
Height of Tree: Height of the tree rooted at some vertex v is the number of edges between the v and the vertex that is farthest from v.
Table of Contents
Example
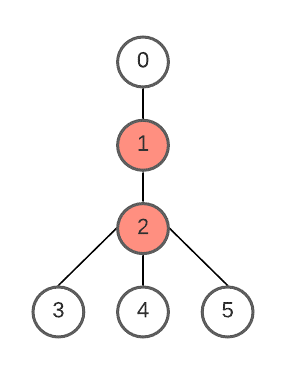
vertices 1 and 2 can form roots with minimum height tree.
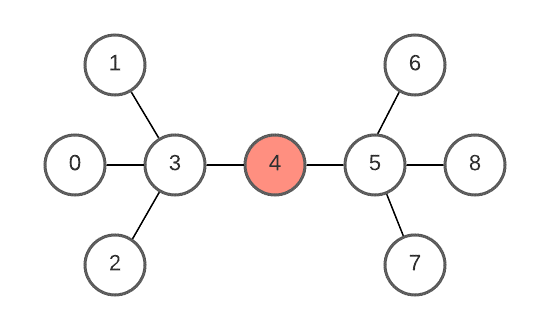
vertex 4 can form root with minimum height tree.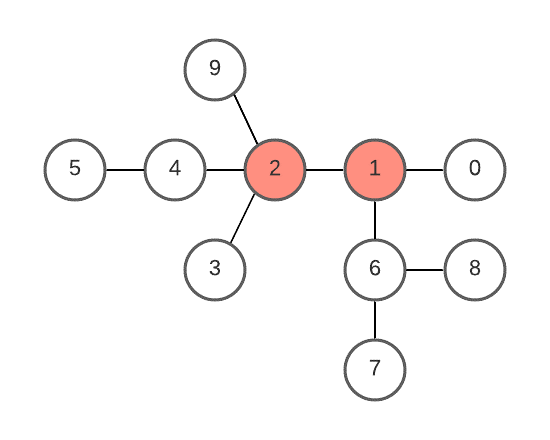
vertices 2 and 1 can form roots with minimum height tree.
Types of solution
- Using the Diameter of the tree.
- BFS based traversal from leaf nodes.
Using the Diameter of the tree
Approach
We find the diameter of the tree, the mid-point of the diameter are minimum height roots. If the length of the diameter is even, the middle two vertices are minimum height roots and if the length is odd the only middle vertex is minimum height root.
Finding the diameter
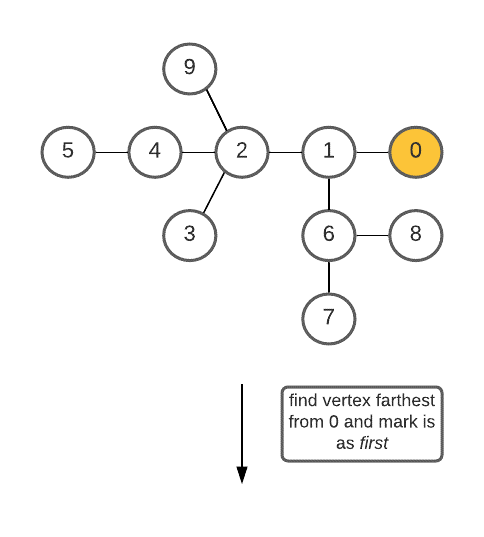
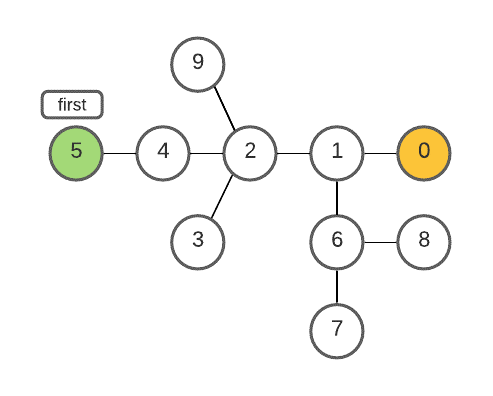
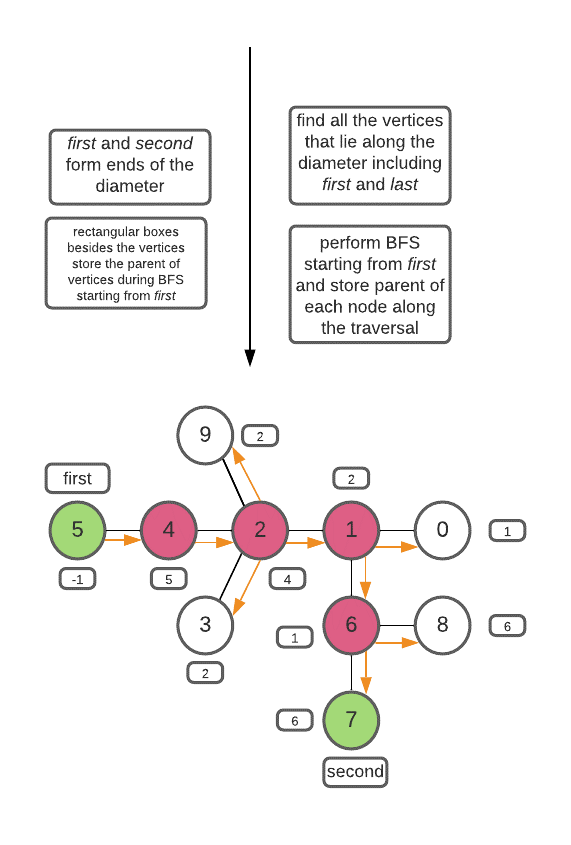
- Choose any random vertex (say vertex with 0 value) and find the vertex (say first ) that is at the largest distance from the vertex chosen. This can be done using BFS/DFS. If there are multiple such vertices that are farthest from the chosen vertex, then take any one of them.
- Now look for the vertex ( say second ) that is at the largest distance from first. This can be done using BFS/DFS. If there are multiple such vertices that are farthest from first, then take any one of them. Now, first and last so obtained from the ends of the diameter.
- Obtain all the elements along the diameter using BFS/DFS including first and last.
After you have obtained the diameter, simply return it’s mid-points.
Algorithm
- Choose any random vertex (say 0).
- Perform BFS from 0 and look for the vertex farthest from it, say first.
- Perform BFS from first and look for the vertex farthest from it, say second.
- first and second form ends of the diameter.
- Again, perform BFS from first and track all the vertices falling along the diameter towards second, this is done by storing parent (predecessor during BFS) of each element along the path.
- return the middle elements(or element) of the diameter.


Implementation
C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
/* function to add edge between nodes u and v */
void addEdge(vector <int> adj[],int u,int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
/* function to perform BFS from a source vertex
and return vertex at largest distance from source */
int BFS(int s,vector <int> adj[],int v)
{
/* define vectors to store visited status
and distance from source vertex */
vector <bool> vis(v,0);
vector <int> dis(v,-1);
queue <int> q;
/* distance of source to itself is 0 */
dis[s] = 0;
q.push(s);
/* begin BFS */
while(!q.empty())
{
int top = q.front();
q.pop();
/* mark current largest as visited */
vis[top] = 1;
for(auto i : adj[top])
{
if(!vis[i])
{
/* mark neighbors of current largest as visited */
vis[i] = 1;
/* update distance of neighbors from current node */
dis[i] = dis[top] + 1;
q.push(i);
}
}
}
/* to store vertex that is at largest distance from source */
int maxVertex;
/* to store largest distance value */
int maxDistance = INT_MIN;
/* find vertex with largest distance from source */
for(int i = 0;i < v;i++)
{
if(dis[i] > maxDistance)
{
maxVertex = i;
maxDistance = dis[i];
}
}
return maxVertex;
}
/* function that return nodes that form root with minimum height */
vector <int> rootMinHeight(vector <int> adj[],int v)
{
/* take any vertex and find vertex at largest distance from it
store it in first */
int first = BFS(0,adj,v);
/* find the vertex at largest distance from first
store it in last */
int last = BFS(first,adj,v);
/* first and last form diameter of the tree and
minimum height vertex/vertices lie at the centre
of diameter */
/* diameter = largest path in a tree */
/* peform BFS from first */
vector <bool> vis(v,0);
/* par store parent of each vertex during BFS traversal
this is used to track the path between first and last (diameter)*/
vector <int> par(v,-1);
queue <int> q;
q.push(first);
/* BFS */
while(!q.empty())
{
int top = q.front();
q.pop();
vis[top] = 1;
for(auto i : adj[top])
{
if(!vis[i])
{
vis[i] = 1;
par[i] = top;
q.push(i);
}
}
}
/* vector to store the diameter of the given tree */
vector <int> largestPath;
/* begin traversal along the diameter starting
from last node towards first node */
while(last != -1)
{
largestPath.push_back(last);
last = par[last];
}
/* result vector to store mid elements of the
diameter, these elements are roots(or root) that form
minimum height trees */
vector <int> result;
int size = largestPath.size();
if(size % 2 == 0)
{
result.push_back(largestPath[(size-1)/2]);
result.push_back(largestPath[size/2]);
}
else
result.push_back(largestPath[size/2]);
return result;
}
/* main function to implement above function */
int main()
{
int v = 10;
vector <int> adj[v];
/* construct the tree */
addEdge(adj,0,1);
addEdge(adj,1,2);
addEdge(adj,2,4);
addEdge(adj,4,5);
addEdge(adj,2,9);
addEdge(adj,2,3);
addEdge(adj,1,6);
addEdge(adj,6,7);
addEdge(adj,6,8);
/* obtain the vertex, that as a root form minimum height tree */
vector <int> result = rootMinHeight(adj,v);
/* root for minimum height tree lie at mid of the diameter */
cout<<"Roots for minimum height tree are : ";
for(auto i : result)
cout<<i<<" ";
return 0;
}Roots for minimum height tree are : 1 2
Java Program
import java.util.*;
import java.io.*;
class tutorialCup
{
/* function to add edge between nodes u and v */
static void addEdge(ArrayList <ArrayList<Integer>> adj,int u,int v)
{
adj.get(u).add(v);
adj.get(v).add(u);
}
/* function to perform BFS from a source vertex
and return vertex at largest distance from source */
static int BFS(int s,ArrayList<ArrayList<Integer>> adj,int v)
{
/* define vectors to store visited status
and distance from source vertex */
ArrayList <Boolean> vis = new ArrayList<>();
ArrayList <Integer> dis = new ArrayList<>();
Queue <Integer> q = new LinkedList<>();
for(int i=0;i<v;i++)
{
vis.add(false);
dis.add(-1);
}
/* distance of source to itself is 0 */
dis.set(s,0);
q.add(s);
/* begin BFS */
while(!q.isEmpty())
{
int top = q.poll();
/* mark current largest as visited */
vis.set(top,true);
Iterator itr = adj.get(top).iterator();
while(itr.hasNext())
{
int i = (Integer)itr.next();
if(!vis.get(i))
{
q.add(i);
dis.set(i,dis.get(top)+1);
vis.set(i,true);
}
}
}
/* to store vertex that is at largest distance from source */
int maxVertex = 0;
/* to store largest distance value */
int maxDistance = Integer.MIN_VALUE;
/* find vertex with largest distance from source */
for(int i = 0;i < v;i++)
{
if(dis.get(i) > maxDistance)
{
maxVertex = i;
maxDistance = dis.get(i);
}
}
return maxVertex;
}
/* function that return nodes that form root with minimum height */
static ArrayList <Integer> rootMinHeight(ArrayList <ArrayList<Integer>> adj,int v)
{
/* take any vertex and find vertex at largest distance from it
store it in first */
int first = BFS(0,adj,v);
/* find the vertex at largest distance from first
store it in last */
int last = BFS(first,adj,v);
/* first and last form diameter of the tree and
minimum height vertex/vertices lie at the centre
of diameter */
/* diameter = largest path in a tree */
/* peform BFS from first */
ArrayList <Boolean> vis = new ArrayList<>();
/* par stores parent of each vertex during BFS traversal
this is used to track the path between first and last (diameter)*/
ArrayList <Integer> par = new ArrayList<>();
for(int i=0;i<v;i++)
{
vis.add(false);
par.add(-1);
}
Queue <Integer> q = new LinkedList<>();
q.add(first);
/* BFS */
while(!q.isEmpty())
{
int top = q.poll();
vis.set(top,true);
Iterator itr = adj.get(top).iterator();
while(itr.hasNext())
{
int i = (Integer)itr.next();
if(!vis.get(i))
{
vis.set(i,true);
par.set(i,top);
q.add(i);
}
}
}
/* vector to store the diameter of the given tree */
ArrayList <Integer> largestPath = new ArrayList<>();
/* begin traversal along the diameter starting
from last node towards first node */
while(last != -1)
{
largestPath.add(last);
last = par.get(last);
}
/* result vector to store mid elements of the
diameter, these elements are roots(or root) that form
minimum height trees */
ArrayList <Integer> result = new ArrayList<>();
int size = largestPath.size();
if(size % 2 == 0)
{
result.add(largestPath.get((size-1)/2));
result.add(largestPath.get(size/2));
}
else
result.add(largestPath.get(size/2));
return result;
}
public static void main (String[] args)
{
int v = 10;
ArrayList <ArrayList<Integer>> adj = new ArrayList<ArrayList<Integer>>();
for(int i=0;i<v;i++)
adj.add(new ArrayList<Integer>());
/* construct the tree */
addEdge(adj,0,1);
addEdge(adj,1,2);
addEdge(adj,2,4);
addEdge(adj,4,5);
addEdge(adj,2,9);
addEdge(adj,2,3);
addEdge(adj,1,6);
addEdge(adj,6,7);
addEdge(adj,6,8);
/* obtain the vertex, that as a root form minimum height tree */
ArrayList <Integer> result = rootMinHeight(adj,v);
/* root for minimum height tree lie at mid of the diameter */
System.out.println("Roots for minimum height tree are : ");
Iterator itr = result.iterator();
while(itr.hasNext())
System.out.print(itr.next()+" ");
}
}Roots for minimum height tree are : 1 2
Complexity Analysis
- Time Complexity : T(n) = O(V+E), but for trees E = V-1, therefore T(n) = O(2V – 1) = O(V).
- Space Complexity : A(n) = O(V).
Using the Diameter of the tree
Approach
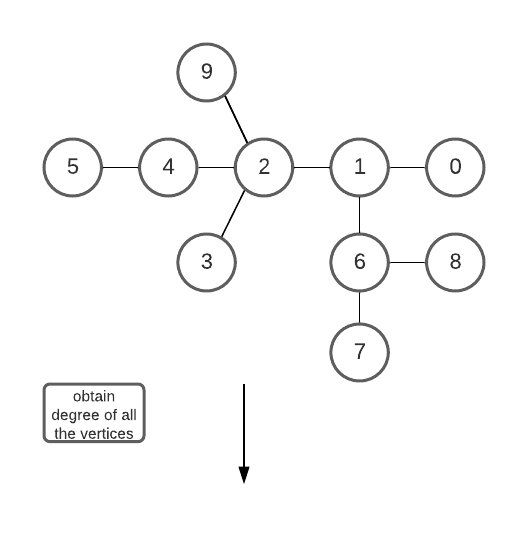
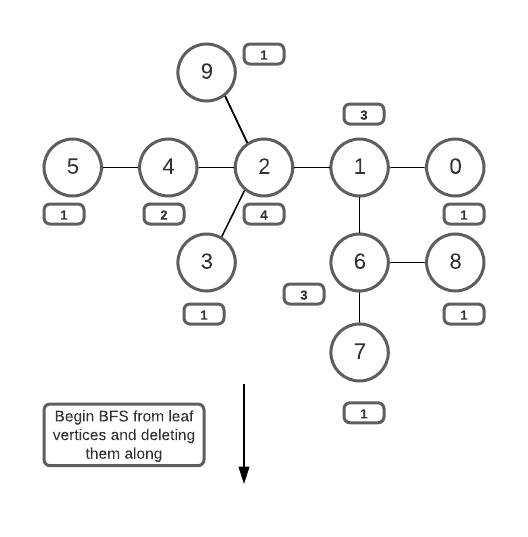
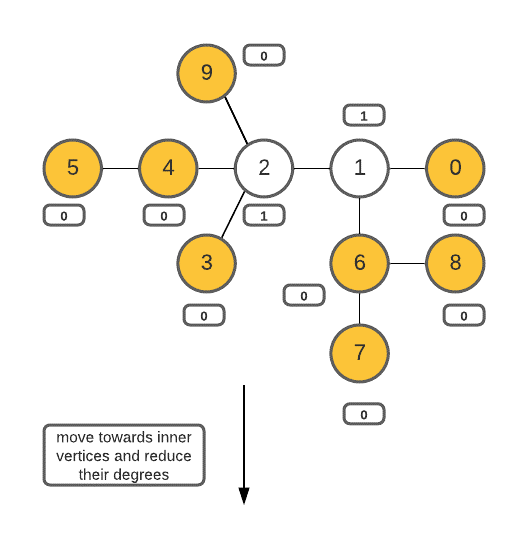
It is to be understood that a tree can only have 1 or 2 vertexes that form root nodes with minimum height. In this approach we perform BFS/DFS traversal from leaf nodes ( nodes that have degree = 1), keep deleting the leaves, and move on to its neighbors. We do this iteratively until only 1 or 2 vertices are left to be deleted. These remaining vertices are the vertices that form root nodes with minimum height.
Degree of a vertex: the degree of a vertex is the number of other vertices it is directly connected to through an undirected edge.
Algorithm
- Create an array that stores the degree of each vertex of the graph.
- Create a queue to perform BFS traversal.
- Identify the leaf vertices (vertices with degree = 1) and push them into the queue.
- Delete these leaves from the graph (mark them as visited) and traverse to their immediate neighbors (and also decrease their degrees by 1 , as they are disconnected with the leaf nodes) using BFS traversal.
- Perform steps 3 and 4 iteratively until only less than 3 vertices are left in the queue.
- These vertices form root nodes with a minimum height of the tree, Store these vertices (or vertex) in an array and return the array.


Implementation
C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
/* function to add edge between nodes u and v */
void addEdge(vector <int> adj[],int u,int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
/* function that return nodes that form root with minimum height */
vector <int> rootMinHeight(vector <int> adj[],int v)
{
/* vector that stores degree of each tree vertex */
vector <int> degree;
queue <int> q;
for(int i=0;i<v;i++)
{
degree.push_back(adj[i].size());
/* push leaf vertex (with degree 1) into the queue */
if(adj[i].size() == 1)
q.push(i);
}
/* begin BFS starting from leaf vertices (and deleting them)
until only 2 or less vertices are left to
be traversed. These vertices left unvisited
form roots with minimum height tree */
while (v > 2)
{
for (int i = 0; i < q.size(); i++)
{
int top = q.front();
q.pop();
v--;
/* for neighbors of the leaf, decrease their degrees
and if those vertices turn out to be leaf vertices
push them into the queue */
for (auto j : adj[top])
{
degree[j]--;
if (degree[j] == 1)
q.push(j);
}
}
}
/* the only vertices (or vertex) remaining in the queue
are the ones that form minimum height tree, store them
into a vector and return the vector */
vector<int> result;
while (!q.empty())
{
result.push_back(q.front());
q.pop();
}
return result;
}
/* main function to implement above function */
int main()
{
int v = 10;
vector <int> adj[v];
/* construct the tree */
addEdge(adj,0,1);
addEdge(adj,1,2);
addEdge(adj,2,4);
addEdge(adj,4,5);
addEdge(adj,2,9);
addEdge(adj,2,3);
addEdge(adj,1,6);
addEdge(adj,6,7);
addEdge(adj,6,8);
/* obtain the vertex, that as a root form minimum height tree */
vector <int> res = rootMinHeight(adj,v);
/* root for minimum height tree lie at mid of the diameter */
cout<<"Roots for minimum height tree are : ";
for(auto i : res)
cout<<i<<" ";
return 0;
}Output
Roots for minimum height tree are : 2 1
Java Program
import java.util.*;
import java.io.*;
class tutorialCup
{
/* function to add edge between nodes u and v */
static void addEdge(ArrayList <ArrayList<Integer>> adj,int u,int v)
{
adj.get(u).add(v);
adj.get(v).add(u);
}
/* function that return nodes that form root with minimum height */
static ArrayList <Integer> rootMinHeight(ArrayList<ArrayList<Integer>> adj, int v)
{
/* vector that stores degree of each tree vertex */
ArrayList <Integer> degree = new ArrayList<>();
Queue <Integer> q = new LinkedList<>();
for(int i=0;i<v;i++)
{
degree.add(adj.get(i).size());
/* push leaf vertex (with degree 1) into the queue */
if(adj.get(i).size() == 1)
q.add(i);
}
/* begin BFS starting from leaf vertices (and deleting them)
until only 2 or less vertices are left to
be traversed. These vertices left unvisited
form roots with minimum height tree */
while (v > 2)
{
for (int i = 0; i < q.size(); i++)
{
int top = q.poll();
v--;
/* for neighbors of the leaf, decrease their degrees
and if those vertices turn out to be leaf vertices
push them into the queue */
Iterator itr = adj.get(top).iterator();
while (itr.hasNext())
{
int j = (Integer)itr.next();
degree.set(j,degree.get(j)-1);
if (degree.get(j) == 1)
q.add(j);
}
}
}
/* the only vertices (or vertex) remaining in the queue
are the ones that form minimum height tree, store them
into a vector and return the vector */
ArrayList <Integer> result = new ArrayList<>();
while (!q.isEmpty())
result.add(q.poll());
return result;
}
public static void main (String[] args)
{
int v = 10;
ArrayList <ArrayList<Integer>> adj = new ArrayList<ArrayList<Integer>>();
for(int i=0;i<v;i++)
adj.add(new ArrayList<Integer>());
/* construct the tree */
addEdge(adj,0,1);
addEdge(adj,1,2);
addEdge(adj,2,4);
addEdge(adj,4,5);
addEdge(adj,2,9);
addEdge(adj,2,3);
addEdge(adj,1,6);
addEdge(adj,6,7);
addEdge(adj,6,8);
/* obtain the vertex, that as a root form minimum height tree */
ArrayList <Integer> res = rootMinHeight(adj,v);
/* root for minimum height tree lie at mid of the diameter */
System.out.println("Roots for minimum height tree are : ");
Iterator itr = res.iterator();
while(itr.hasNext())
System.out.print(itr.next()+" ");
}
}Roots for minimum height tree are : 2 1
Complexity Analysis
- Time Complexity : T(n) = O(V+E), but for trees E = V-1, therefore T(n) = O(2V – 1) = O(V).
- Space Complexity : A(n) = O(V).