K-th Smallest Element in a Sorted Matrix

Difficulty Level Medium
Frequently asked in Amazon Facebook Google
Array Binary Search Heap MatrixViews 5628

In K-th Smallest Element in a Sorted Matrix problem, we have given an n x n matrix, where every row and column is sorted in non-decreasing order. Find the kth smallest element in the given 2D array.

Example

Input 1:
k = 3 and 
matrix =
        11, 21, 31, 41
        16, 26, 36, 46
        25, 30, 38, 49
        33, 34, 40, 50
Ouput: 21
Explanation: The 3rd smallest element = 21 


Input 2:
k = 7 and 
matrix =
        12, 23, 31
        17, 27, 36
        24, 29, 38
Ouput: 31
Explanation: The 7th smallest element is 30

Types of Solution for K-th Smallest Element in a Sorted Matrix

  1. Naive/Brute Force
  2. using min Heap data structure
  3. Binary Search

Naive/Brute Force

Approach

This approach involves simply adding all the elements of the matrix into an array, sorting the array and returning the k-th smallest number.

Algorithm for K-th Smallest Element in a Sorted Matrix

  1. given a matrix mat[][] of dimensions n x n, create a linear array arr[] of size n*n.
  2. Add all the elements of mat into the arr.
  3. Sort arr and return arr[k-1] (k-th largest element).

Implementation for K-th Smallest Element in a Sorted Matrix

C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;

// function to find k-th largest element
int kthSmallest(vector < vector<int> > mat,int k)
{
    int n = mat.size();
    
    if(k > n*n)
    return -1;
    
    // smallest element is the first element of the matrix
    if(k == 1)
    return mat[0][0];
    
    // define array and push contents of the matrix into it
    vector <int> arr;
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
        arr.push_back(mat[i][j]);
    
    // sort the array and obtain k-th smallest element
    sort(arr.begin(),arr.end());
    
    return arr[k-1];
}

int main() 
{
  vector< vector<int> > mat {
                              {11, 21, 31, 41},
                              {16, 26, 36, 46},
                              {25, 30, 38, 49},
                              {33, 34, 40, 50}
                              };
  
  int k = 3;
  int kthsmall = kthSmallest(mat,k);
  
    if(kthsmall == -1)
    cout<<"3rd smallest element doesn't exist.";
    else
    cout<<"3rd smallest element = "<<kthsmall<<endl;
  
  return 0;
}
3rd smallest element = 21
Java Program
import java.io.*;
import java.util.*;

class tutorialCup 
{
    // function to find k-th largest element
    static int kthSmallest(ArrayList<ArrayList<Integer>> mat,int k)
    {
        int n = mat.size();
        
        if(k > n*n)
        return -1;
        
        // smallest element is the first element of the matrix
        if(k == 1)
        return mat.get(0).get(0);
        
        // define array and push contents of the matrix into it
        ArrayList <Integer> arr = new ArrayList <Integer>();
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)
            arr.add(mat.get(i).get(j));
        
        // sort the array and obtain k-th smallest element
        Collections.sort(arr);
        
        return arr.get(k-1);
    }

    public static void main (String[] args) 
    {
    	ArrayList<ArrayList<Integer>> mat = new ArrayList<ArrayList<Integer>>();
    	mat.add(new ArrayList<Integer>(Arrays.asList(11, 21, 31, 41)));
    	mat.add(new ArrayList<Integer>(Arrays.asList(16, 26, 36, 46)));
    	mat.add(new ArrayList<Integer>(Arrays.asList(25, 30, 38, 49)));
    	mat.add(new ArrayList<Integer>(Arrays.asList(33, 34, 40, 50)));
    	                            
    	int k = 3;
    	int kthsmall = kthSmallest(mat,k);
    	
        if(kthsmall == -1)
        System.out.println("3rd smallest element doesn't exist.");
        else
        System.out.println("3rd smallest element = "+kthsmall);
    	
    }    
}
3rd smallest element = 21

Complexity Analysis

  1. Time Complexity : T(n) = O(n2)
  2. Space Complexity : A(n) = O(n2)

Using min Heap data structure

Approach

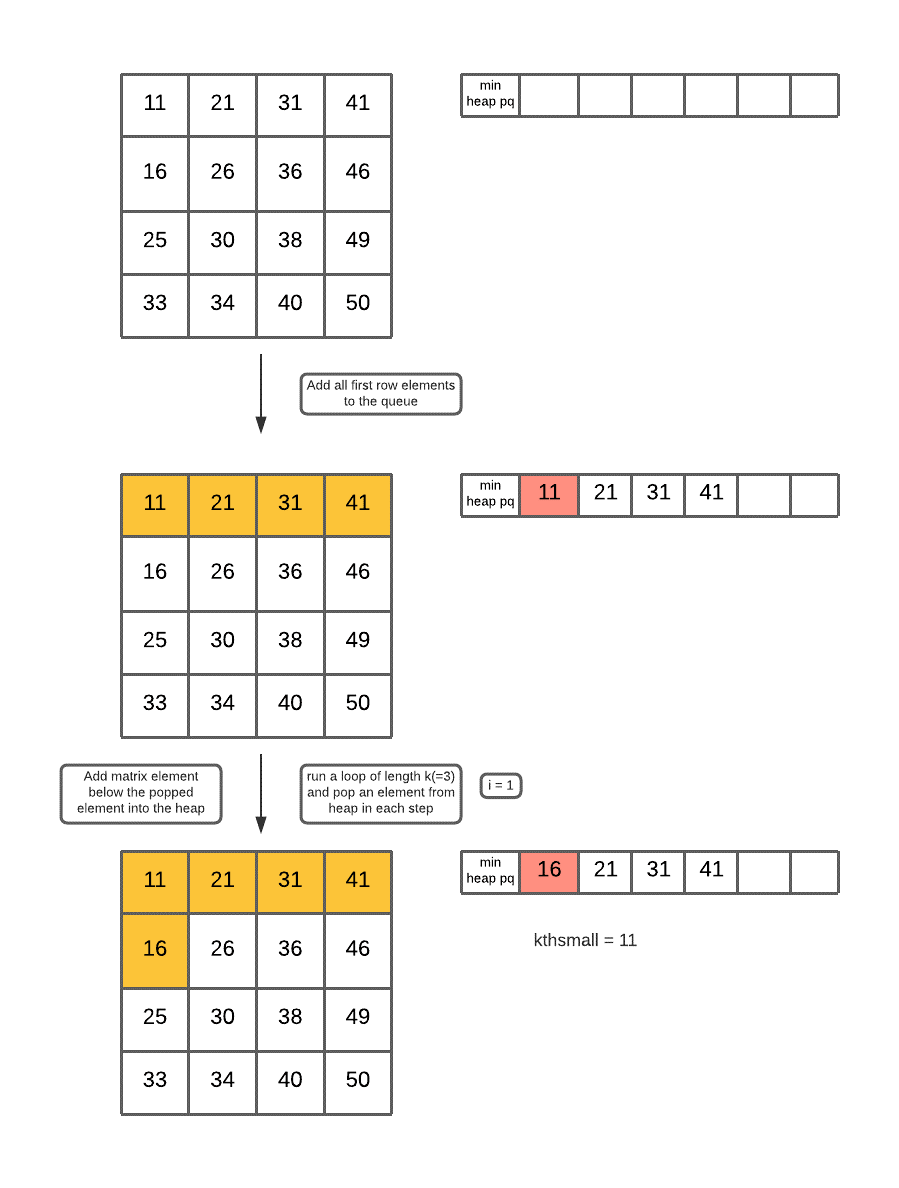
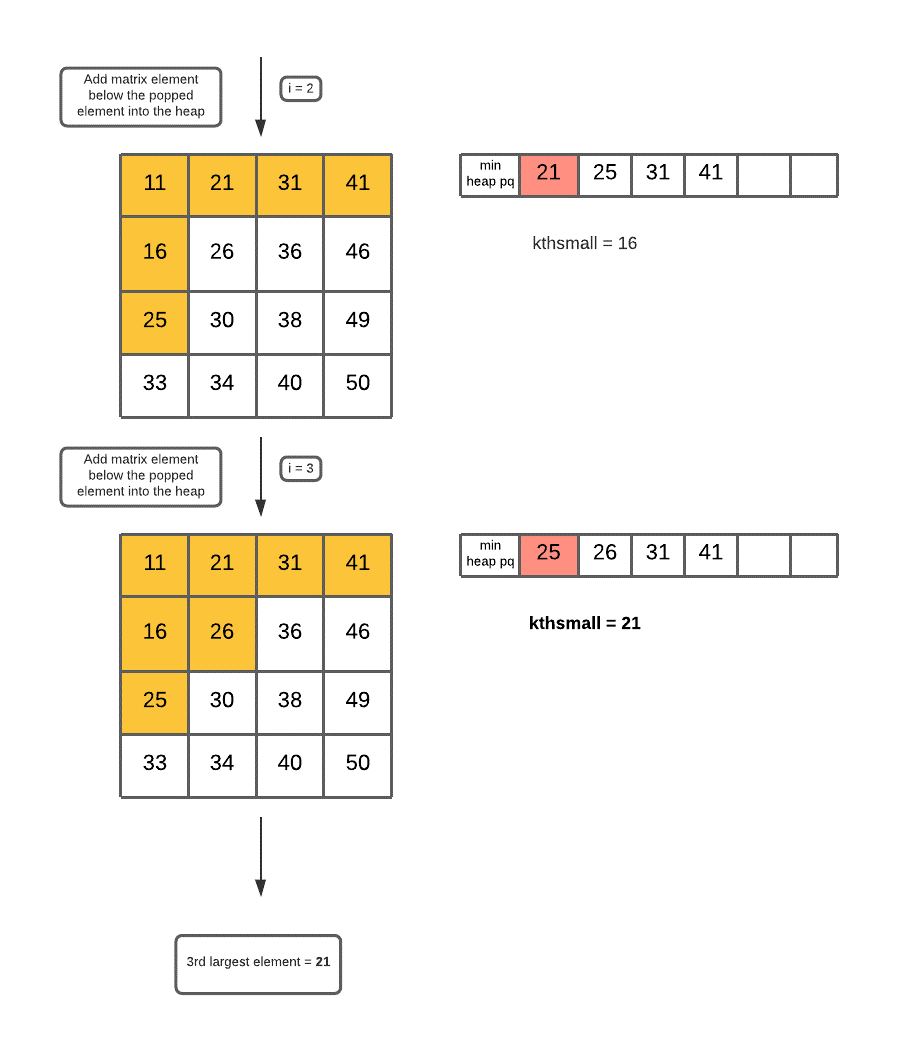
we use heap data structure(priority queue/min heap) to store the elements of the first row of the matrix, then one by one pop elements from the heap and add the element from the matrix lying just below the last popped element. This is done until k-steps obtain k-th largest number. The algorithm is discussed below :

Algorithm for K-th Smallest Element in a Sorted Matrix

  1. deal with the base cases explicitly(n = 0,1).
  2. define a min-heap pq.
  3. add the elements from the first row of mat[][] (input matrix) into pq.
  4. Now, run a loop k-times.  the loop variable is i, inside that loop perform steps below :
    • pop an element from pq and store the popped element into kthsmall.
    • add the element lying in mat[][] just below kthsmall into pq.
  5. After the loop ends, return the last element value stored in kthsmall (ie kthsmall.num).

K-th Smallest Element in a Sorted MatrixK-th Smallest Element in a Sorted Matrix

Implementation for K-th Smallest Element in a Sorted Matrix

C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;

// define a strucure 
// to store a particular value from the matrix
// it's row and column number
struct element
{
    int num;
    int i;
    int j;
    
    // define constructors
    element(){}
    element(int element,int rownum,int colnum)
    {
        num = element;
        i = rownum;
        j = colnum;
    }
};

// this is an strucure which implements the 
// operator overlading 
// this will help us in creating a heap for storing
// values of element(struct) data type
struct compare 
{ 
    bool operator()(element const& p1, element const& p2) 
    { 
        return p1.num > p2.num; 
    } 
}; 

// function to find k-th largest element
int kthSmallest(vector < vector<int> > mat,int k)
{
    int n = mat.size();
    
    if(k > n*n)
    return -1;
    
    // smallest element is the first element of the matrix
    if(k == 1)
    return mat[0][0];
    
    // define a min Heap
    priority_queue <struct element,vector <element>,compare > pq;
    
    // push all the elements of first row
    // along with their row and column numbers
    // into a min heap
    for(int i=0;i<n;i++)
    {
        struct element curr(mat[0][i],0,i);
        pq.push(curr);
    }
    
    // define a variable to process each value stored in min heap
    struct element kthsmall;
    
    // pop from heap for k steps
    for(int i=0;i<k;i++)
    {
        kthsmall = pq.top();
        pq.pop();
        
        // if last popped element lies in the last row\
        // dont need to push any number
        if(kthsmall.i+1 >= n)
        {
            struct element curr(INT_MAX,-1,-1);
            pq.push(curr);
        }
        /* push the element below (element in the same column as the element itself)
        the last element popped from the minheap*/ 
        else
        {
            struct element curr(mat[kthsmall.i + 1][kthsmall.j],kthsmall.i+1,kthsmall.j);
            pq.push(curr);
        }
    }
    
    // return the element last popped from the heap pq
    return kthsmall.num;
    
}

int main() 
{
  vector< vector<int> > mat {
                              {11, 21, 31, 41},
                              {16, 26, 36, 46},
                              {25, 30, 38, 49},
                              {33, 34, 40, 50}
                              };
  
  int k = 3;
  int kthsmall = kthSmallest(mat,k);
  
    if(kthsmall == -1)
    cout<<"3rd smallest element doesn't exist.";
    else
    cout<<"3rd smallest element = "<<kthsmall<<endl;
  
  return 0;
}
3rd smallest element = 21
Java Program
import java.io.*;
import java.util.*;

/*
define a strucure 
to store a particular value from the matrix
it's row and column number
*/
public class element
{
    public int num;
    public int i;
    public int j;
    
    public element(){}
    
    public element(int element,int rownum,int colnum)
    {
        num = element;
        i = rownum;
        j = colnum;
    }
    
    public int numReturn()
    {
        return num;
    }
}

class tutorialCup 
{
    // function to find k-th largest element
    static int kthSmallest(ArrayList<ArrayList<Integer>> mat,int k)
    {
        int n = mat.size();
    
        if(k > n*n)
        return -1;
        
        // smallest element is the first element of the matrix
        if(k == 1)
        return mat.get(0).get(0);
        
        // Comparator forms heap using num attribute of object of element type
        // sorts the heap using obj.num value
        // where obj is an object of element type
        Comparator<element> sorter = Comparator.comparing(element::numReturn);
        // define a min Heap
        PriorityQueue <element> pq = new PriorityQueue<element>(sorter);
        
        // push all the elements of first row
        // along with their row and column numbers
        // into a min heap
        for(int i=0;i<n;i++)
        {
            element curr = new element(mat.get(0).get(i),0,i);
            pq.add(curr);
        }
        
        // define a variable to process each value stored in min heap
        element kthsmall = new element();
        
        // pop from heap for k steps
        for(int i=0;i<k;i++)
        {
            kthsmall = pq.peek();
            pq.poll();
            
            // if last popped element lies in the last row\
            // dont need to push any number
            if(kthsmall.i+1 >= n)
            {
                element curr = new element(Integer.MAX_VALUE,-1,-1);
                pq.add(curr);
            }
            /* push the element below (element in the same column as the element itself)
            the last element popped from the minheap*/ 
            else
            {
                element curr = new element(mat.get(kthsmall.i + 1).get(kthsmall.j),kthsmall.i+1,kthsmall.j);
                pq.add(curr);
            }
        }
    
        // return the element last popped from the heap pq
        return kthsmall.num;
    }

    public static void main (String[] args) 
    {
    	ArrayList<ArrayList<Integer>> mat = new ArrayList<ArrayList<Integer>>();
    	mat.add(new ArrayList<Integer>(Arrays.asList(11, 21, 31, 41)));
    	mat.add(new ArrayList<Integer>(Arrays.asList(16, 26, 36, 46)));
    	mat.add(new ArrayList<Integer>(Arrays.asList(25, 30, 38, 49)));
    	mat.add(new ArrayList<Integer>(Arrays.asList(33, 34, 40, 50)));
    	                            
    	int k = 3;
    	int kthsmall = kthSmallest(mat,k);
    	
        if(kthsmall == -1)
        System.out.println("3rd smallest element doesn't exist.");
        else
        System.out.println("3rd smallest element = "+kthsmall);
    	
    }    
}
3rd smallest element = 21

Complexity Analysis

  1. Time Complexity : T(n) = O(n + klogn)
  2. Space Complexity : A(n) = O(n)

Binary Search

Approach

We can Apply Binary Search on the matrix mat[][], however, this is different from a conventional binary search as in this case we consider “number range”(matrix values itself) instead of the “index range”. As we know that the smallest number of our matrix is at the top left corner and the biggest number is at the bottom lower corner. These two numbers can represent the “range” i.e., the lo and the hi values for the Binary Search. below we explain how we implement our algorithm.

Algorithm for K-th Smallest Element in a Sorted Matrix

  1. Start the Binary Search with lo = mat[0][0] and hi = mat[n-1][n-1].
  2. Find mid of the lo and the hi. This middle number is NOT necessarily an element in the matrix.
  3. Count all the numbers smaller than or equal to mid in the matrix. As the matrix is sorted, we can do this in O(N).
  4. If the count is less than ‘K’, we can update lo = mid+1 to search in the higher part of the matrix
  5. Else if the count is greater than or equal to ‘K’, we can update hi = mid to search in the lower part of the matrix in the next iteration.
  6. At some point lo and hi become equal in values and the loop terminates. lo contains the value of k-th smallest element as we iteratively narrowed down our search range to a single matrix element.

Implementation for K-th Smallest Element in a Sorted Matrix

C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;

// function to find k-th largest element
int kthSmallest(vector < vector<int> > mat,int k)
{
    int n = mat.size();
        
    if(k == 0 || k > n*n || n == 0)
    return -1;
    
    if(k == 1)
    return mat[0][0];
    
    // define smallest and largest element in the matrix as
    // lower range &
    // upper range
    int lo = mat[0][0];
    int hi = mat[n-1][n-1];
    
    // perform binary search (by value)
    // between smallest(top-left) and largest(bottom-down) values
    while (lo < hi) 
    {
        int mid = lo + (hi - lo) / 2;
        int count = 0;
        int j = n - 1;
        
        // find out how many numbers are greater than mid
        // between lo and hi
        for (int i = 0; i < n; i++) 
        {
            while (j >= 0 && mat[i][j] > mid) 
                j--;
                
            count += (j + 1);
        }
        
        // if number of such element is less than k
        // narrow the search range by increasing lo value
        if (count < k) 
            lo = mid + 1;
        // if number of such element is greater or equal to k
        // narrow the search range by decreasing hi value
        else 
            hi = mid;
    } 
    
    // after iteratively narrowing the search range
    // you narrow down to a single element in the matrix
    // which is k-th smallest element
    return lo;
}

int main() 
{
  vector< vector<int> > mat {
                              {11, 21, 31, 41},
                              {16, 26, 36, 46},
                              {25, 30, 38, 49},
                              {33, 34, 40, 50}
                              };
  
  int k = 3;
  int kthsmall = kthSmallest(mat,k);
  
    if(kthsmall == -1)
    cout<<"3rd smallest element doesn't exist.";
    else
    cout<<"3rd smallest element = "<<kthsmall<<endl;
  
  return 0;
}
3rd smallest element = 21
Java Program
import java.io.*;
import java.util.*;

class tutorialCup 
{
    // function to find k-th largest element
    // this function performs a binary search by value
    // on the given matrix
    static int kthSmallest(ArrayList<ArrayList<Integer>> mat,int k)
    {
        int n = mat.size();
        
        if(k == 0 || k > n*n || n == 0)
        return -1;
        
        if(k == 1)
        return mat.get(0).get(0);
        
        // define smallest and largest element in the matrix as
        // lower range &
        // upper range
        int lo = mat.get(0).get(0);
        int hi = mat.get(n-1).get(n-1);
        
        // perform binary search (by value)
        // between smallest(top-left) and largest(bottom-down) values
        while (lo < hi) 
        {
            int mid = lo + (hi - lo) / 2;
            int count = 0;
            int j = n - 1;
            
            // find out how many numbers are greater than mid
            // between lo and hi
            for (int i = 0; i < n; i++) 
            {
                while (j >= 0 && mat.get(i).get(j) > mid) 
                    j--;
                    
                count += (j + 1);
            }
            
            // if number of such element is less than k
            // narrow the search range by increasing lo value
            if (count < k) 
                lo = mid + 1;
            // if number of such element is greater or equal to k
            // narrow the search range by decreasing hi value
            else 
                hi = mid;
        } 
        
        // after iteratively narrowing the search range
        // you narrow down to a single element in the matrix
        // which is k-th smallest element
        return lo;
    }

    public static void main (String[] args) 
    {
    	ArrayList<ArrayList<Integer>> mat = new ArrayList<ArrayList<Integer>>();
    	mat.add(new ArrayList<Integer>(Arrays.asList(11, 21, 31, 41)));
    	mat.add(new ArrayList<Integer>(Arrays.asList(16, 26, 36, 46)));
    	mat.add(new ArrayList<Integer>(Arrays.asList(25, 30, 38, 49)));
    	mat.add(new ArrayList<Integer>(Arrays.asList(33, 34, 40, 50)));
    	                            
    	int k = 3;
    	int kthsmall = kthSmallest(mat,k);
    	
        if(kthsmall == -1)
        System.out.println("3rd smallest element doesn't exist.");
        else
        System.out.println("3rd smallest element = "+kthsmall);
    	
    }    
}
3rd smallest element = 21

Complexity Analysis

  • Time Complexity : T(n) = O(nlog(max-min)) = O(nlog(const)) = O(n), here max-min is the difference between largest and smallest values in the matrix.Since both are integers, the maximum difference can’t be more than INT_MAX, so essentially max-min becomes constant.
  • Space Complexity : A(n) = O(1)

References

Translate »