In Symmetric Tree problem we have given a binary tree, check whether it is a mirror of itself. A tree is said to be a mirror image of itself if there exists an axis of symmetry through a root node that divides the tree into two same halves.
Table of Contents
Example
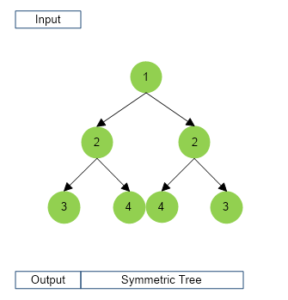

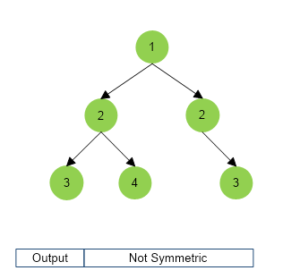
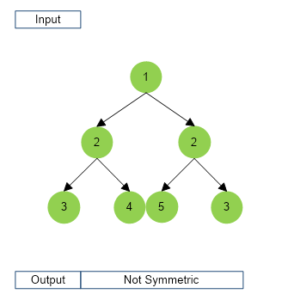
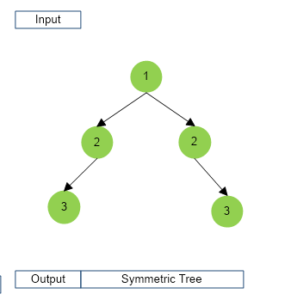
Types of Solution for Symmetric Tree
- Recursive
- Iterative
Recursive
Approach
We use 2 copies of the binary tree say, b1 and b2(to handle left and right subtree separately) and check if :
- root value of b1 and b2 are the same or not.
- left subtree of b1 and right subtree of b2 are the same(in terms structure as well as node values) or not.
- right subtree of b1 and left subtree of b2 is the same(in terms structure as well as node values) or not.
if conditions 1,2 and 3 are true recursively for left and right subtrees we simply return true (else return false).
b1 and b2 have root1 and root2 as root node respectively.
Algorithm for Symmetric Tree
- Create two copies of the binary tree (root1 and root2) to handle the left and right subtree separately.
- Define the base case.
- Check if conditions mentioned above (1,2 and 3) are true or not.
- If the above conditions are false, meaning that either of root1 or root2 is empty, then return false.
Implementation for Symmetric Tree
C++ Program for Symmetric Tree
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// defining the tree node
class Node
{
public :
int data;
Node *left;
Node *right;
// constructor for initialization
Node(int num)
{
data = num;
left = right = NULL;
}
};
/*utility function to check whether trees rooted at
root1 and root2 are mirror images of each other or not */
bool utility(Node *root1, Node *root2)
{
/* base case : if both trees are empty then
they are mirror images of each other */
if (root1 == NULL && root2 == NULL)
return true;
/* for trees rooted at root1 and root2 to be mirror images,
following conditions must be satisfied */
if (root1 && root2)
/* Their root node's data must be same
if this is not the case then immediately
return false */
return root1->data == root2->data &&
/*left subtree of left tree and right s
ubtree of right tree have to be mirror images*/
utility(root1->left, root2->right) &&
/*right subtree of left tree and left subtree
of right tree have to be mirror images*/
utility(root1->right, root2->left);
/* This condition is reached when :
if only either of root1 or root2 is empty */
return false;
}
/* function to check if tree
rooted at root is Symmetric */
bool isSymmetric(Node* root)
{
// apply utility function to check if tree is mirror of itself
return utility(root, root);
}
// main function to implement above functions
int main()
{
/* construct the binary tree*/
Node *root = new Node(1);
root->left = new Node(2);
root->right = new Node(2);
root->left->left = new Node(3);
root->left->right = new Node(4);
root->right->left = new Node(4);
root->right->right = new Node(3);
isSymmetric(root) ? cout<<"Symmetric Tree" : cout<<"Not Symmetric";
return 0;
}Symmetric Tree
Java program for Symmetric Tree
import java.io.*;
import java.util.*;
class tutorialCup
{
static class Node
{
int data;
Node left;
Node right;
Node(int num)
{
data = num;
left = right = null;
}
};
/*utility function to check whether trees rooted at
root1 and root2 are mirror images of each other or not */
static boolean utility(Node root1, Node root2)
{
/* base case : if both trees are empty then
they are mirror images of each other */
if (root1 == null && root2 == null)
return true;
/* for trees rooted at root1 and root2 to be mirror images,
following conditions must be satisfied */
if (root1 != null && root2 != null)
/* Their root node's data must be same
if this is not the case then immediately
return false */
return root1.data == root2.data &&
/*left subtree of left tree and right s
ubtree of right tree have to be mirror images*/
utility(root1.left, root2.right) &&
/*right subtree of left tree and left subtree
of right tree have to be mirror images*/
utility(root1.right, root2.left);
/* This condition is reached when :
if only either of root1 or root2 is empty */
return false;
}
/* function to check if tree
rooted at root is Symmetric */
static boolean isSymmetric(Node root)
{
// apply utility function to check if tree is mirror of itself
return utility(root, root);
}
/* main function to implement above function */
public static void main (String[] args)
{
/* construct the binary tree*/
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(2);
root.left.left = new Node(3);
root.left.right = new Node(4);
root.right.left = new Node(4);
root.right.right = new Node(3);
if(isSymmetric(root))
System.out.println("Symmetric Tree");
else System.out.println("Not Symmetric");
}
}Symmetric Tree
Complexity Analysis
- Time Complexity : T(n) = O(n)
- Space Complexity : A(n) = O(1) or O(log n), considering recursion stack space.
Iterative
Approach
The idea is to convert the recursive approach into iterative approach by using a Queue data structure by performing a breadth-first search(BFS)/level order traversal. Again, We use 2 copies of the binary tree say, b1 and b2(to handle left and right subtree separately) and check if :
- root value of b1 and b2 are the same or not.
- left subtree of b1 and right subtree of b2 are the same(in terms structure as well as node values) or not.
- right subtree of b1 and left subtree of b2 are the same(in terms structure as well as node values) or not.
if conditions 1,2 and 3 are true Iteratively true for left and right subtrees we simply return true (else return false).
b1 and b2 have root1 and root2 as root node respectively.
Algorithm for Symmetric Tree
- Define base cases.
- Create a queue and push two copies of root (to handle left and right subtree) node into it.
- Begin The BFS traversal and at each iteration pop two nodes from the queue namely leftNode and rightNode.
- if the value of both the nodes is not equal then return false (and terminate the traversal).
- Then, if leftNode.left and rightNode.right both are not null, push them into the queue.
- if only either of the above is not null then return false (and terminate the traversal).
- Then, if leftNode.right and rightNode.left both are not null, push them into the queue.
- if only either one of the above is not null then return false (and terminate the traversal).
- If the queue becomes empty, BFS is terminated and returns true.
Example 1



Example 2


Implementation for Symmetric Tree
C++ Program for Symmetric Tree
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// defining the tree node
class Node
{
public :
int data;
Node *left;
Node *right;
// constructor for initialization
Node(int num)
{
data = num;
left = right = NULL;
}
};
/* function to check if tree
rooted at root is Symmetric */
bool isSymmetric(Node* root)
{
/* base cases */
// 1. if tree is empty it's symmetric
if(root == NULL)
return true;
// 2. if tree has only one node, it's symmetric
if(!root->left && !root->right)
return true;
// create queue for BFS traversal
queue <Node*> q;
/* root is inserted two times so that we can peform
bi-directional BFS to check mirror image property
which is basically a type of bilateral symmetry */
q.push(root);
q.push(root);
/* these store nodes for bi-directional BFS traversal */
Node* leftNode, *rightNode;
while(!q.empty())
{
/* remove nodes to check if they are symmetric or not */
leftNode = q.front();
q.pop();
rightNode = q.front();
q.pop();
/* if both left and right nodes exist but
have different, the tree is not symmetric */
if(leftNode->data != rightNode->data)
return false;
/* Push left child of left subtree node
and right child of right subtree
node in queue */
if(leftNode->left && rightNode->right)
{
q.push(leftNode->left);
q.push(rightNode->right);
}
/* Else if only one child is present alone
and other is NULL, then tree is not symmetric */
else if (leftNode->left || rightNode->right)
return false;
/* Push right child of left subtree node
and left child of right subtree node
in queue */
if(leftNode->right && rightNode->left)
{
q.push(leftNode->right);
q.push(rightNode->left);
}
/* Else if only one child is present alone
and other is NULL, then tree is not symmetric */
else if(leftNode->right || rightNode->left)
return false;
}
/* the tree is symmetric if all the nodes
have been processed and queue becomes empty */
return true;
}
// main function to implement above functions
int main()
{
/* construct the binary tree*/
Node *root = new Node(1);
root->left = new Node(2);
root->right = new Node(2);
root->left->left = new Node(3);
root->left->right = new Node(4);
root->right->left = new Node(4);
root->right->right = new Node(3);
isSymmetric(root) ? cout<<"Symmetric Tree" : cout<<"Not Symmetric";
return 0;
}Symmetric Tree
Java program for Symmetric Tree
import java.io.*;
import java.util.*;
class tutorialCup
{
static class Node
{
int data;
Node left;
Node right;
Node(int num)
{
data = num;
left = right = null;
}
};
/* function to check if tree
rooted at root is Symmetric */
static boolean isSymmetric(Node root)
{
/* base cases */
// 1. if tree is empty it's symmetric
if(root == null)
return true;
// 2. if tree has only one node, it's symmetric
if(root.left == null && root.right == null)
return true;
// create queue for BFS traversal
Queue <Node> q = new LinkedList<>();
/* root is inserted two times so that we can peform
bi-directional BFS to check mirror image property
which is basically a type of bilateral symmetry */
q.add(root);
q.add(root);
/* these store nodes for bi-directional BFS traversal */
Node leftNode, rightNode;
while(!q.isEmpty())
{
/* remove nodes to check if they are symmetric or not */
leftNode = q.poll();
rightNode = q.poll();
/* if both left and right nodes exist but
have different, the tree is not symmetric */
if(leftNode.data != rightNode.data)
return false;
/* Push left child of left subtree node
and right child of right subtree
node in queue */
if(leftNode.left != null && rightNode.right != null)
{
q.add(leftNode.left);
q.add(rightNode.right);
}
/* Else if only one child is present alone
and other is NULL, then tree is not symmetric */
else if (leftNode.left != null || rightNode.right != null)
return false;
/* Push right child of left subtree node
and left child of right subtree node
in queue */
if(leftNode.right != null && rightNode.left != null)
{
q.add(leftNode.right);
q.add(rightNode.left);
}
/* Else if only one child is present alone
and other is NULL, then tree is not symmetric */
else if(leftNode.right != null || rightNode.left != null)
return false;
}
/* the tree is symmetric if all the nodes
have been processed and queue becomes empty */
return true;
}
/* main function to implement above function */
public static void main (String[] args)
{
/* construct the binary tree*/
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(2);
root.left.left = new Node(3);
root.left.right = new Node(4);
root.right.left = new Node(4);
root.right.right = new Node(3);
if(isSymmetric(root))
System.out.println("Symmetric Tree");
else System.out.println("Not Symmetric");
}
}Symmetric Tree
Complexity Analysis
- Time Complexity : T(n) = O(n)
- Space Complexity : A(n) = O(n),queue is used.