Find Peak Element

Let’s understand Find Peak Element problem. Today we have with us an array that needs its peak element. Now, you must be wondering as to what do I mean by the peak element? The peak element is one which is greater than all its neighbours.

Example: Given an array of [1,2,3,1]

Peak element: 3

Let us understand that better by an image representation

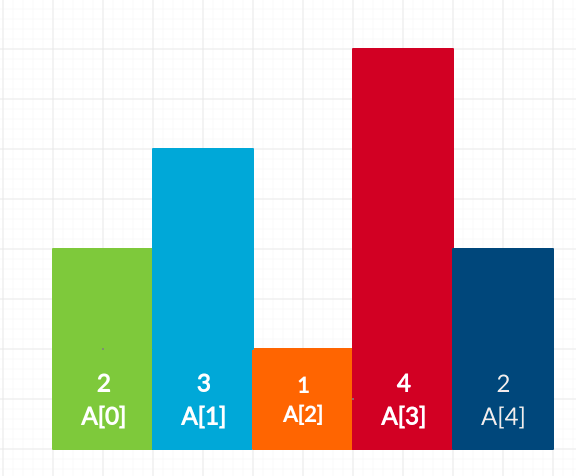
The above image shows perfectly how 4 stands out from its neighbouring elements to make it to the peak element. The challenge before us now is how we approach the given problem.

Approach-1

Brute Force For Find Peak Element

The standard observation we can make from the image is returning the maximum element (the one that stands out) in the entire array.

Let us skim through the process of finding the maximum element from the array

• Maintain a max variable. Put the value as the 0th element from the array in it initially.
• Maintain a variable to store the index. Here,j.
• Run a loop through the entire array
  • Every time we encounter a value greater than max
    • Update the variable max
    • Put in the new index value in j
• Return j

C++ Code For Find Peak Element

class Solution 
{
public:
    int findPeakElement(vector<int>& nums) 
    {
     int max=nums[0];
     int pos=0;
     for(int i=0;i<nums.size();i++)
     {
      if(max<nums[i]) 
      {
          max=nums[i];
          pos=i;
      }
     }
    return pos;    
    }
};

7
1 3 8 2 1 5 3

2

Java Code For Find Peak Element

class Solution 
{
    public int findPeakElement(int[] nums) 
    {
     int max=nums[0];
     int pos=0;
     for(int i=0;i<nums.length;i++)
     {
      if(max<nums[i]) 
      {
          max=nums[i];
          pos=i;
      }
     }
    return pos;
    }
}

5
-10 1 0 10 5

3

Time Complexity of the approach=O(n)

We live in an era where everything can be made faster. So, why not this solution?

Let us take it from the top and make it O(log n)

Approach-2

Binarizing The Search

Now that we have exhausted our linear means let us bring to the picture Binary the mother of all things log(n).

What do we do here?

• Maintain two pointers high and low
• Calculate the midpoint using the pointers
  • Every time the mid element is greater than the element adjacent to it
    • We start making a search in the first half of the array searching for the element that might be greater
    • Why?
      • The second half has definitely handed over their peak to the first half betraying our rule of being greater
  • Every time the mid element is smaller than the element adjacent to it
    • We start making a search in the second half of the array searching for the element that might be greater than it’s neighbours
    • Why?
      • The first half has definitely handed over their peak to the second half betraying our rule of being greater
  • Keep repeating it until the low ends up being greater than high
  • Return the element is contained at the low position as it is which consists of the Peak Element 

Java Code

class Solution 
{
    public int findPeakElement(int[] nums) 
    {
    int low=0;
     int hig=nums.length-1;
     while(hig>low)
     {
         int mid=low+(hig-low)/2;
         if(nums[mid]>nums[mid+1])
             hig=mid;
         else
             low=mid+1;
     }
     return low;    
    }
}

5
10 11 0 10 5

1

C++ Code

class Solution 
{
    public:
    int findPeakElement(vector<int>& nums) 
    {
     int low=0;
     int hig=nums.size()-1;
     while(hig>low)
     {
         int mid=low+(hig-low)/2;
         if(nums[mid]>nums[mid+1])
             hig=mid;
         else
             low=mid+1;
     }
     return low;    
    }
};

5
0 1 0 14 5

1

The Time complexity of the above approach = O(log n)

Space Complexity = O(1)

References

Don’t stop learning and catch up with us on with one of the most interesting sorting techniques:

Insertion Sort