Problem description : you are given n integers (y0, y1, y2 … yn-1) at n indices (i = 0,1,2 … n-1). Integer at i-th index is yi. Now, you draw n lines on a cartesian plane each connecting points (i, yi) and (i, 0). Find the maximum volume of water that can be stored between two pairs of lines, together with the x-axis forming a container.
Since the lines are represented in a 2D plane, the volume of water can be calculated by calculating the area of 2D space in which the water is stored.
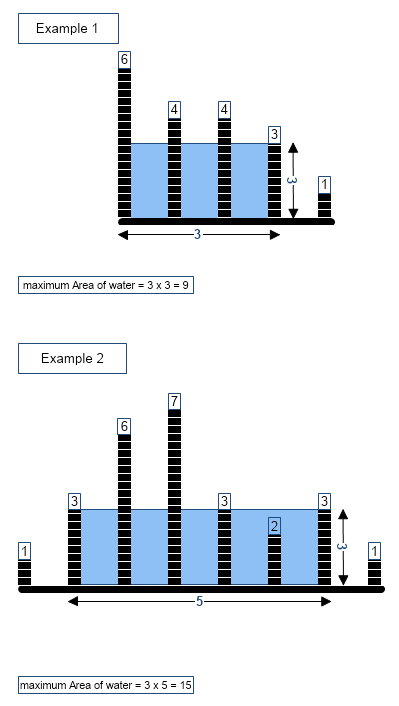
Example 1
Input: arr[] = [6, 4, 4, 3, 1] Output: 9
Example 2
Input: arr[] = [1, 3, 6, 7, 3, 2, 3, 1] Output: 15
Table of Contents
Types of solution For Container with Most Water
- Naive
- Two pointer Algorithm
Naive Solution
Approach
we simply take each pair of lines and find the area between them and return the maximum.number of pairs generated = n(n+1)/2.
Algorithm
- define a nested loop.
- Outer loop traverses the arr[] from 0 to n-2, index of the loop is i.
- Inner loop traverses the arr[] from i+1 to n-1, index of the loop is j.
- for each pair of i and j, calculate the area contained between arr[i] and arr[j].
- Area between each pair is given by maxArea = min(arr[i],arr[j]) * (j – i).
- Store the maximum of all such values of area calculated and return it.
Implementation
C++ Program For Container with Most Water
#include <iostream>
#include<bits/stdc++.h>
using namespace std;
// function to find maximum water stored.
int maxWater(int arr[],int n)
{
int maxArea = 0;
for(int i=0;i<n-1;i++)
{
for(int j=i+1;j<n;j++)
maxArea = max(maxArea,min(arr[i],arr[j])*(j-i));
}
return maxArea;
}
// main function to implement above functions
int main()
{
int arr[] = {1, 3, 6, 7, 3, 2, 3, 1};
int n = sizeof(arr)/sizeof(arr[0]);
cout<<"Maximum water stored = "<<maxWater(arr,n)<<endl;
return 0;
}
Output
Maximum water stored = 15
Java Program For Container with Most Water
import java.io.*;
import java.util.*;
public class tutorialcup
{
// function to find maximum water stored.
static int maxWater(int arr[],int n)
{
int maxArea = 0;
for(int i=0;i<n-1;i++)
{
for(int j=i+1;j<n;j++)
maxArea = Math.max(maxArea,Math.min(arr[i],arr[j])*(j-i));
}
return maxArea;
}
// main program to implement above functions
public static void main (String[] args)
{
int arr[] = {1, 3, 6, 7, 3, 2, 3, 1};
int n = arr.length;
System.out.println("Maximum water stored = "+maxWater(arr,n));
}
}Output
Maximum water stored = 15
Complexity Analysis
- Time complexity : T(n) = O(n2), nested loops used.
- Space complexity : A(n) = O(1)
Two pointer algorithm
Approach
A better time efficient approach to solve this problem is to use two markers (or pointers) that point to first and last element of the array.
The algorithm is discussed below :
Algorithm For Container with Most Water
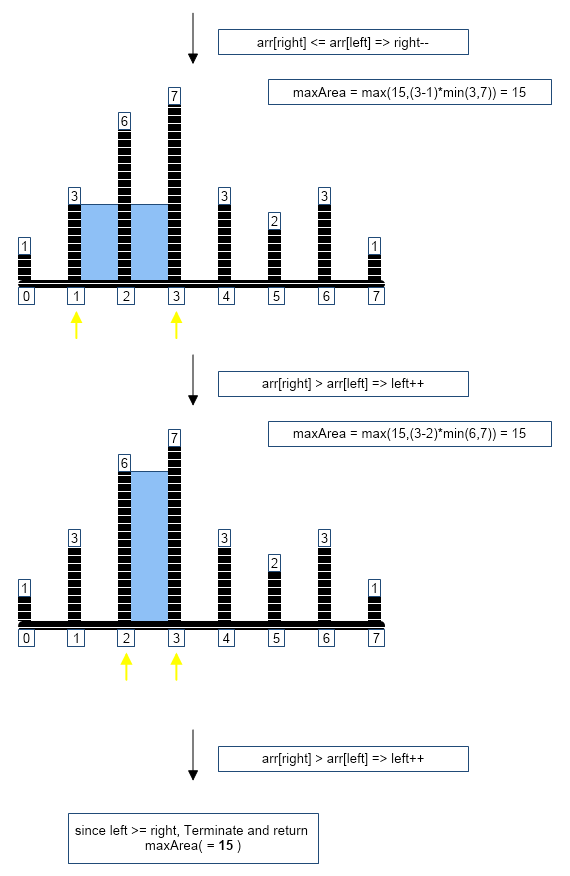
- define two markers left = 0 and right = n-1,left points to first element and right points to last element of the array respectively.
- define a variable maxArea that stores the maximum area (and so the volume) of the water.
- increment left and decrement right until right is greater than the left.
- At each step calculate the area of water stored between left and right as area = (min(arr[left],arr[right])*(right-left).
- Store maximum of all the values of area calculated in maxArea and return it.


Implementation
C++ Program For Container with Most Water
#include <iostream>
#include<bits/stdc++.h>
using namespace std;
// function to find maximum water stored.
int maxWater(int arr[],int n)
{
int maxArea = 0;
int left = 0,right = n-1;
while(left < right)
{
maxArea = max(maxArea,min(arr[left],arr[right])*(right-left));
if(arr[left] < arr[right])
left++;
else
right--;
}
return maxArea;
}
// main function to implement above functions
int main()
{
int arr[] = {1, 3, 6, 7, 3, 2, 3, 1};
int n = sizeof(arr)/sizeof(arr[0]);
cout<<"Maximum water stored = "<<maxWater(arr,n)<<endl;
return 0;
}
Output
Maximum water stored = 15
Java Program For Container with Most Water
import java.io.*;
import java.util.*;
class tutorialcup
{
// function to find maximum water stored.
static int maxWater(int arr[],int n)
{
int maxArea = 0;
int left = 0,right = n-1;
while(left < right)
{
maxArea = Math.max(maxArea,Math.min(arr[left],arr[right])*(right-left));
if(arr[left] < arr[right]) left++;
else right--;
}
return maxArea;
}
// main program to implement above functions
public static void main (String[] args)
{
int arr[] = {1, 3, 6, 7, 3, 2, 3, 1};
int n = arr.length;
System.out.println("Maximum water stored = "+maxWater(arr,n));
}
}Output
Maximum water stored = 15
Complexity Analysis
- Time complexity : T(n) = O(n), only single traversal through array occurs.
- Space complexity : A(n) = O(1)