In the previous post(Graph and its implementation, BFS of a graph and DFS of a graph) we understand the logic and the implementation of the Graph traversal. Now we look forward and see the application and needs of the BFS/DFS.
Table of Contents
Application of the Breadth-First-Search
Connected Components of a given Graph using BFS
A connected component of a given graph is defined as the set of nodes of a given graph such that each pair of the node connected by a path. Point to note that all pair of the connected component is distinct and union of all sets(connected components) will be equal to the total number of vertices. There are 4 connected components of the below graph:
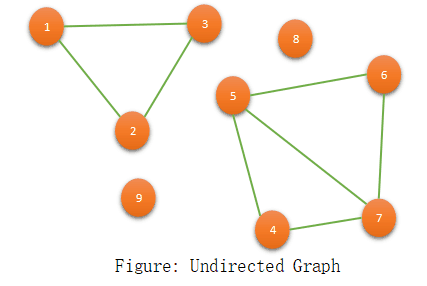
To find out the connected component of a given graph we use BFS/DFS for all the vertices which are unvisited. Let’s see the pseudo-code for both logic using BFS and DFS.
Print the connected component of a given graph and each set of vertices for a connected component separated by a new line.
There are two approaches-
Using BFS:
Step:1 Set all vertices as unvisited(false).
Step:2 Traverse all the vertices of the graph and perform the following operation:
a) If the current vertex is unvisited then call DFS_CALC(vertex_v).
b) Move to the next line(use endl).
BFS_CALC(vertex_v):
Step:1 Inserting vertex_v in queue and mark as visited.
Step:2 Process till queue.empty()==false
a) Find the first element of the queue and pop it and store it in the top variable.
b) Processing all the connected vertex of the top:
i) for all connected vertex(c_v) of top in graph:
if(c_v is unvisited) then: queue.push(c_v) and mark c_v as visited.
Using DFS:
Step:1 Set all vertices as unvisited(false).
Step:2 Traverse all the vertices of the graph and perform the following operation:
a) If the current vertex is unvisited then call DFS_CALC(current vertex).
b) Move to the next line (use endl).
DFS_CALC(vertex_v):
Step:1 Print vertex_v.
Step:2 Mark vertex_v as visited(true).
Step:3 Now call DFS_CALC(u) for every connected vertex(u) to vertex_v and if the connected vertex(u) is unvisited.Check a graph is Bipartite or not using BFS
A bipartite graph is those graph which has partition the vertices into two sets A, B. Every edge has one vertex in A and another vertex in B. In other words, we also say that there is no edge between the vertices of set A or B where A union B = V(Set of all vertices of the graph) and A intersection B = NULL. Let see the example for better understanding:
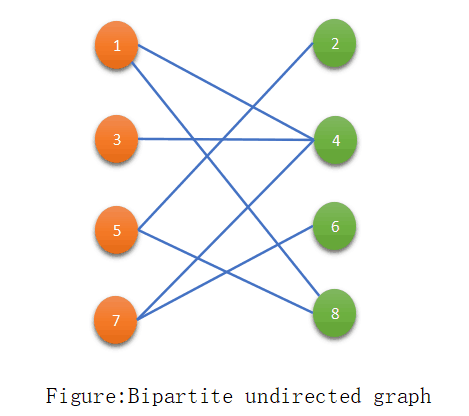
The set A of the vertices of the above graph is {1,3,5,7} and set B of the vertices of the above graph is {2,4,6,8}.
We use BFS to find the graph is Bipartite or not by assign 0,1 to the vertices. Were 0 for set A and 1 for set B and after assigning we check whether two vertices having the same assigned value contain edge or not. If no edge found between vertices has the same value(0,1) then we say that the graph is Bipartite. Let’s see the pseudo-code for the above logic:
Pseudo-Code Step:1 Assign 0 to the starting vertex(source vertex) and put it into set A. Step:2 Set 1 for all the neighbors of the previous vertex(of set A) and putting them into set B. Step:3 Set 0 to all the neighbor's neighbor. Step:4 Follow the above process until we assign (0,1) to all the vertices. Step:5 While assigning the values if we find edges between the vertices whose assigned value is the same then the print graph is "not bipartite".
Cycle detection in the undirected graph using BFS
We use a Queue data structure for cycle detection. When we apply BFS at a vertex and find any connected node(to the visited node) which is present in the queue then we say that graph contains a cycle. Let’s see the example for better understanding:

Here we see that the current vertex which is visited is 5 and we also see 4 is present in the queue already and also the connected vertex of 5. Then we say that there is a cycle in the given graph(Here 3-4-5-3 is only the cycle present in the graph).
Pseudo-Code:
Step:1 Apply BFS to all the unvisited vertex of the graph.
Step:2 If we find any connected node(wrt current vertex) which is already visited and not the parent of
the current vertex then we say that there is a cycle in graph otherwise no cycle in the graph.Shortest path for Unweighted Graph using BFS
We use BFS to find out the shortest path for the unweighted graph. While applying BFS we store the predecessor of the given vertices. This logic will also work for the negative weights cycles present in the graph. Find out the shortest path between 1-7. Here 1-2-4-7 and 1-2-5-7 are two shortest paths having length 3.
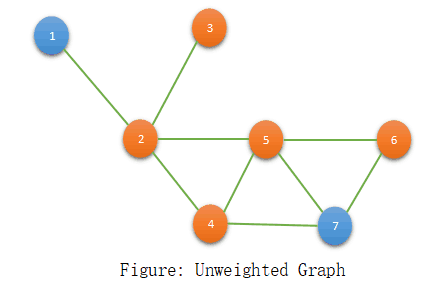
Let’s see the pseudo-code of the logic:
Pseudo-Code:
Step:1 Set all the vertices as unvisited(visited[v]=false).
Step:2 Set distance for all vertices as infinity(distance[v]=INF).
Step:3 Set predecessor of every vertex as -1(predecessor[v]=-1).
Step:4 Now first vertex to be visited.
i) set visited[start]=true.
ii) distance[start]=0 because the distance between the start to start is 0.
iii) queue.push(start).
Step:5 While(!queue.empty()) then:
i) Read a vertex(front) from the queue.
ii) For all connected vertices of front which are unvisited:
a) Make it visited.
b) The distance of connected vertex is: distance[front]+1.
c) Predecessor of connected vertex is front(predecessor[front][i]=front).
d) queue.push(v[front][i]) where v[front][i] is connected vertex of front.
e) if(destination==v[front][i]) then return true.
Step:6 return false.
Step:7 Print the length of the shortest path by print distance[destination].
Step:8 Print the path of the shortest path by print the predecessor from the destination to starting.There are some other applications of BFS also:
- Social Networking Websites(Like Facebook).
- GPS navigation systems.
- Broadcasting in the network.
- Peer to Peer Networks.
- Used in Garbage Collection.
- Crawlers in Search Engines.
- Path Finding.
- Ford-Fulkerson Algorithm.
Application of the Depth-First-Search
Path Finding using DFS
Through the use of DFS, we find out the path between two vertices. Just apply the DFS at the first vertex and check whether we reach to the second vertex by using dfs traversal.
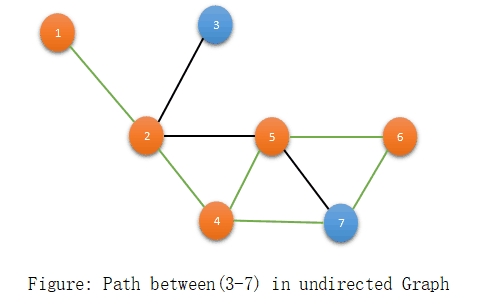
Pseudo-Code: Step:1 Call DFS(start) where start as the first vertex. Step:2 Use a stack to store the path between start vertex to current vertex. Step:3 If(second_vertex==curent_vertex) then return the path using stack.
Topological Sorting using DFS
It’s an arrangement of vertices such that every directed edge uv from vertex u to v, u come before vertex v in the ordering. Here is some point to remember before using the concept of topological sorting:
a) The graph should be DAG(Direct acyclic graph).
b) Every DAG will have one and more than one topological ordering.
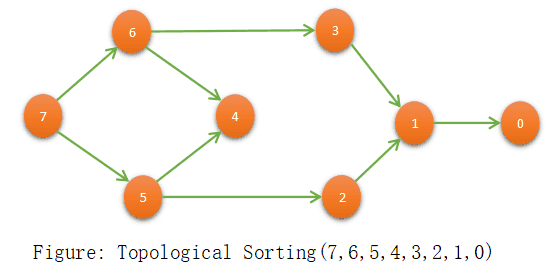
Pseudo-Code:
Step:1 vector ord that will contain the sorted nodes.
Step:2 Set all nodes as unvisited(false).
Step:3 While exists nods are unvisited then:
select an unvisited node v and call topological(v).
topological(v):
Step:1 If v is visited then return.
Step:2 If v is unvisited then stop.
Step:3 Set v as unvisited(false).
Step:4 If u is the connected vertex of v then call topological(u) for all possible value of u.
Step:5 Set v as visited(true).
Step:6 Add v to the vector ord.
Step:7 Print vector ord.Find a strongly connected component of the graph using DFS
If we are able to traverse between any pair of nodes by some path in the connected component of a graph is called strongly connected. Let’s see the example and pseudo-code for the logic to find the strongly connected component of a graph.
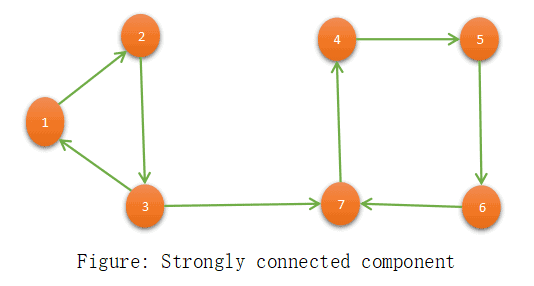
The following are the SCC of the graph (0,2,1) and (6,5,4,3).
Pseudo-Code:
Step:1 Apply DFS(start) on the graph and store the finishing time of each node.
DFS(start):
i) visited[start]=true.
ii) for all neighbours u of start that are unvisited:
DFS(u).
iii) stack.push(u).
Step:2 Reverse the graph.
i) Clear the adjacency list.
ii) for all edges between u to v:
adjacency_list[v].push_back(u).
Step:3 Apply DFS from the vertex which is on the top of the stack.
While(!stack.empty()):
i) top=stack.top().
ii) stack.pop().
DFS(u).
iii) if top is unvisited:
DFS(top).
Step:4 When all nodes which are visited will form SCC.
Step:5 Repeat till we get a vertex from the top of the stack which is unvisited.There are some other applications of DFS also:
- Find the minimum spanning tree.
- Check whether a graph bipartite or not.
- Solving puzzles with only one solution.
- Finding the bridges of a graph.
- Planarity testing.
- Finding connectivity in the graphs.
- Finding the spanning forest in the graph.