Dijkstra is the shortest path algorithm. Dijkstra algorithm is used to find the shortest distance of all nodes from the given start node. It logically creates the shortest path tree from a single source node, by keep adding the nodes greedily such that at every point each node in the tree has a minimum distance from the given start node.
Dijkstra algorithm is a greedy approach that uses a very simple mathematical fact to choose a node at each step.
“Adding two positive numbers will always results in a number greater than both inputs”.
Table of Contents
Algorithm
Here is the Dijkstra algorithm
Variables used
- n: number of nodes.
- e: number of edges.
- visited, an array of size n to keep track of nodes that are added in the tree.
- cost, an array of size n to store the minimum cost to reach the ith node from start node via a valid path in the tree.
Steps
- Initialize visited array with false which shows that currently, the tree is empty.
- Initialize cost array with infinity which shows that it is impossible to reach any node from the start node via a valid path in the tree.
- The cost to reach the start node will always be zero, hence cost[start]=0.
- Now at every iteration we choose a node to add in the tree, hence we need n iterations to add n nodes in the tree:
- Choose a node that has a minimum cost and is also currently non-visited i.e., not present in the tree.
- Update the cost of non-visited nodes which are adjacent to the newly added node with the minimum of the previous and new path.
- Mark the node as visited.
Example of Dijkstra Algorithm
Given a graph, compute the minimum distance of all nodes from A as a start node.

Step by Step Solution of Dijkstra Algorithm

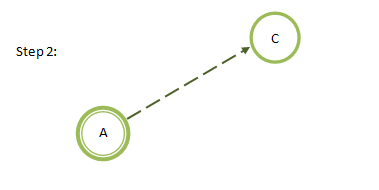
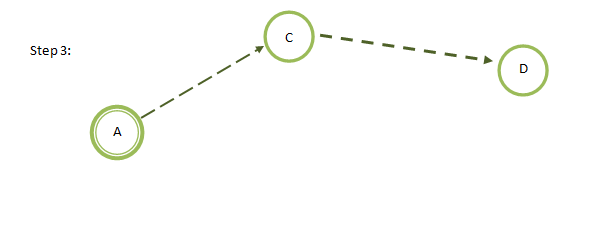
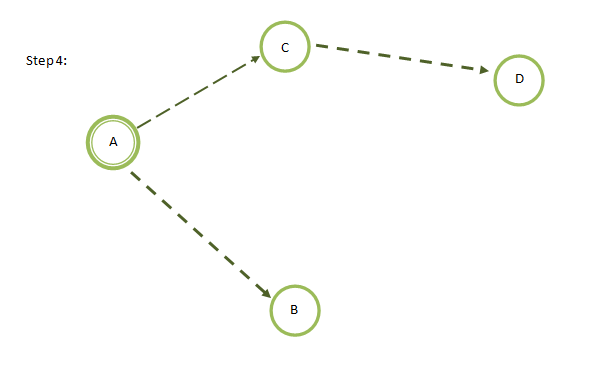

Disadvantage of Dijkstra Algorithm
As we know the basic property used in Dijkstra is the addition of two positive numbers, hence, this algorithm may lead to the wrong answer in the case of the graph containing negative edges.
Example
Consider the graph

Starting node: A
Dijkstra will compute 3 as minimum distance to reach B from A.
But we can clearly see A->C->E->B path will cost 2 to reach B from A.
Question on Dijkstra Algorithm
Given a directed weighted graph with n nodes and e edges, your task is to find the minimum cost to reach each node from the given start node
Input
The first line of input contains two integer n (number of edges) and e (number of edges).
The next e lines contain three space-separated integers u, v and w where:
- u: source node
- v: destination node
- w: weight of the edge
The last line contains s, denoting start node
Constraints
1<=n<=1000
0<=e<=(n*(n-1))/2
1<=weight<=103
The graph contains no self-loop and multiple edges.
C++ Code for Dijkstra Algorithm
#include<bits/stdc++.h>
#define INF INT_MAX
using namespace std;
// Function to find the non-visited node which is at minimum distance
int findMin(int n,int cost[],bool visited[]){
int min=INF;
int node=0;
for(int i=0;i<n;i++){
if(visited[i]==false && min>cost[i]){
min=cost[i];
node=i;
}
}
return node;
}
void dijkstra(int n, vector<pair<int,int>> graph[], int start){
bool visited[n]; // to specify which nodes are yet to visit
int cost[n]; // cost[i] specifies the minimum cost to reach ith node from start node through visited nodes
for(int i=0;i<n;i++){
cost[i]=INF; // initialize cost array with INFINITY
// to signify that all nodes are non-reachable initially
visited[i]=false; // initialize visited array with false
// to signify that all nodes are non-visited initially
}
cost[start]=0; // minimum cost to reach the start node will be zero
int count=0; // count will keep track of how many nodes are visited till now
while(count<n){
int node = findMin(n,cost,visited);
visited[node]=true;
for(auto &i:graph[node]){
if(visited[i.first]==false){
cost[i.first]=min(cost[i.first],cost[node]+(i.second));
}
}
count++;
}
for(int i=0;i<n;i++){
cout<<"Distance of node "<<i<<" from node "<<start<<" is "<<cost[i]<<"\n";
}
}
int main(){
int n,e;
cin>>n>>e;
vector<pair<int,int>> graph[n];
for(int i=0;i<e;i++){
int u,v,w;
cin>>u>>v>>w;
graph[u].push_back(make_pair(v,w));
graph[v].push_back(make_pair(u,w));
}
int start;
cin>>start;
dijkstra(n,graph,start);
}
5 7 0 2 5 0 1 3 2 3 2 3 4 5 2 4 1 4 1 4 2 3 7 0
Distance of node 0 from node 0 is 0 Distance of node 1 from node 0 is 3 Distance of node 2 from node 0 is 5 Distance of node 3 from node 0 is 7 Distance of node 4 from node 0 is 6
Java Code for Dijkstra Algorithm
import java.util.Scanner;
public class Main {
public static int [][] graph;
public static int [] visited;
public static int [] cost;
public static int start;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n,e, INF = Integer.MAX_VALUE;
n = sc.nextInt();
e = sc.nextInt();
graph = new int [n][n];
visited = new int [n];
cost = new int[n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
graph[i][j] = -1;
}
}
for (int i = 0; i < e; i++) {
int u = sc.nextInt();
int v = sc.nextInt();
int w = sc.nextInt();
graph[u][v] = w;
graph[v][u] = w;
}
start = sc.nextInt();
for (int i = 0; i < n; i++) {
cost[i]=INF;
}
cost[start]=0;
dijkstra(start);
printResult();
}
/* Recursive function to find the minimum distance of each node from given start node*/
public static void dijkstra(int start){
for (int i = 0; i <cost.length; i++) {
if (graph[start][i] > -1 && cost[i] > (graph[start][i] + cost[start]) ){
cost[i] = graph[start][i] + cost[start];
}
}
int j = minDist();
if (j == -1 )
return;
visited[j] = 1;
dijkstra(j);
}
/* Function to print the distance of each node from given start node*/
public static void printResult(){
for (int i = 0; i <cost.length; i++) {
System.out.println("Distance of node "+i+" from node "+start+" is "+cost[i]);
}
}
/* Function to find non-visited node with minimum distance*/
public static int minDist(){
int minDistance = Integer.MAX_VALUE;
int index = -1;
for (int i=0; i<cost.length; i++){
if (minDistance>cost[i] && visited[i] == 0){
minDistance = cost[i];
index = i;
}
}
return index;
}
}Input: 4 5 0 1 12 0 3 24 2 0 3 1 3 10 3 2 12 0
Output: Distance of node 0 from node 0 is 0 Distance of node 1 from node 0 is 12 Distance of node 2 from node 0 is 3 Distance of node 3 from node 0 is 15
Time complexity: O(n*n)
The time complexity of Dijkstra algorithm can be improved using binary heap to choose the node with minimum cost (step 4)
Go through more interview questions