Everyone might be wondering. Argh, another new MINIMAX ALGORITHM.
Why do we need it? Let’s know to play a game of chess or tic-tac-toe we have often wondered if there was an algorithm to win the game.
Table of Contents
Explanation
A lot of times we might have wondered if
- It was possible to decipher the moves of the opponent
- It was possible to play optimally
MiniMax Algorithm brings in just the thing for us!
In a search tree for a two-player game, there can be two kinds of nodes
- MAX Nodes
- These are the nodes representing the move you can make
- Represented as upward-pointing triangles
- The goal of these nodes: Maximizing the value of subtree under the node
- Value of max node: Value of child with the maximum value
- These are the nodes representing the move you can make
- MIN Nodes
- These are the nodes representing the moves your opponent can make
- Represented as downward-pointing triangles
- The Goal of these nodes: Minimizing the value of subtree under the node
- Value of min node: Value of child with the minimum value
- These are the nodes representing the moves your opponent can make
A lot of this might not be making sense to you.
Let’s understand that by an example
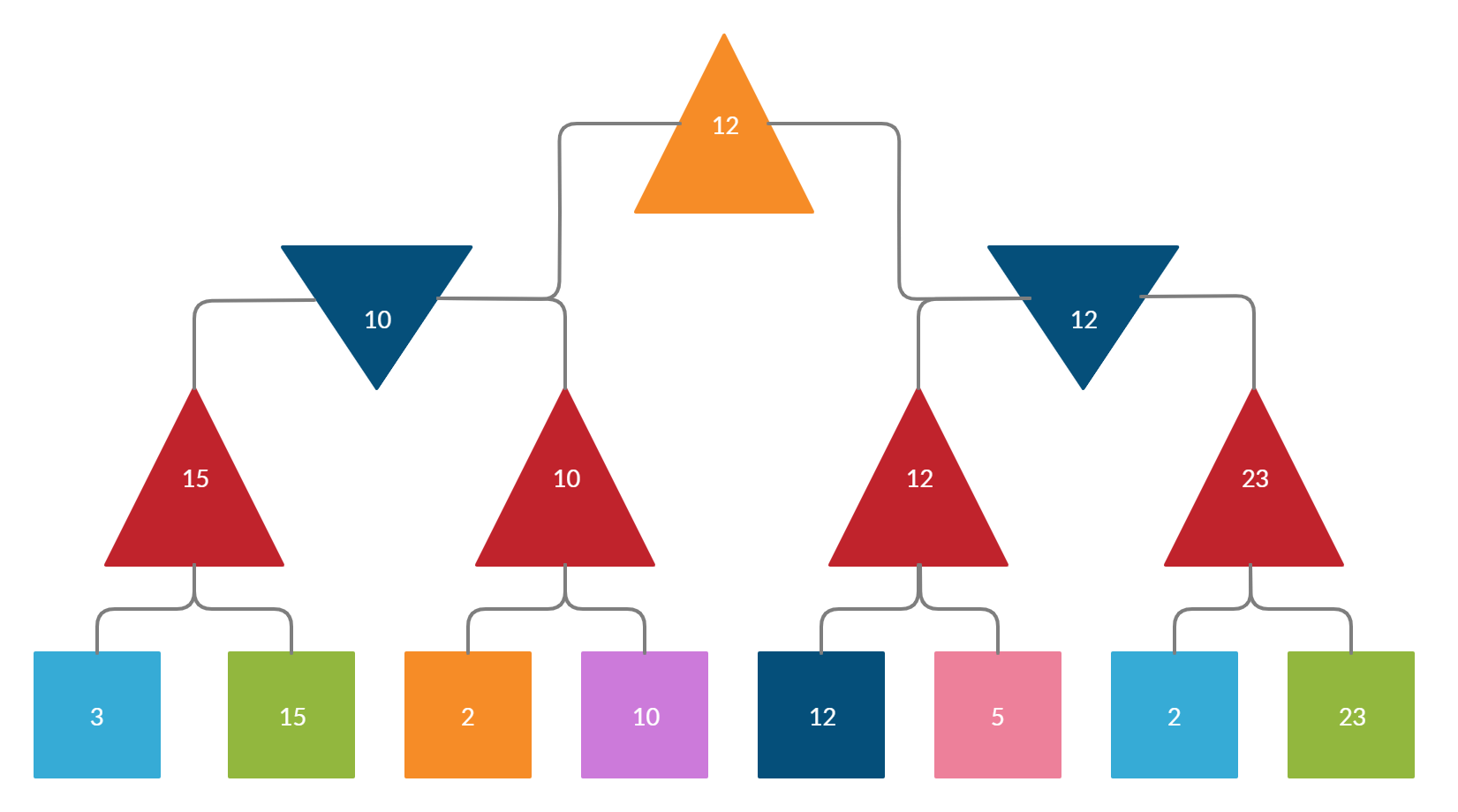
Assume we have 8 initial states with the values as shown in the figure below
- Initially, we take the max of each one of two nodes
- Ex-From 3 and 15 we find the max
- We put this max value in the max node(Upward pointing triangles)
- Once the max cycle is completed we take the min from the max nodes
- Ex-From 15 and 10 we take 10
- We put this min value in the min node(Downward pointing triangle)
- Keep repeating this until we reach/finalize a value
Backtracking all the possible moves we make a decision choosing the values accordingly and reaching up to the conclusion
Let’s understand it better by a code snippet
Java Code for Minimax Algorithm
import java.io.*;
import java.util.*;
public class minimax
{
public static int decide(int cur,int index,boolean max,int weight[],int height)
{
int num=0;
//If we reach a leaf node
if(cur==height)
return weight[index];
//If the node is a max one we find the max from sub-nodes
if(max)
num=Math.max(decide(cur+1,index*2,false,weight,height),decide(cur+1,index*2+1,false,weight,height));
//If it is a min node we minimize the value under the sub-tree
else
num=Math.min(decide(cur+1,index*2,true,weight,height),decide(cur+1,index*2+1,true,weight,height));
return num;
}
public static void main(String args[])
{
int scor[] = {3, 15, 2, 10, 12, 5, 2, 23};
int n= scor.length;
int h= (int)(Math.log(n) / Math.log(2));
int a=decide(0,0,true,scor,h);
System.out.println(a);
}
}C++ Code for Minimax Algorithm
#include<iostream>
#include<cmath>
using namespace std;
int max(int a,int b)
{
if(a>b)
return a;
else
return b;
}
int min(int a,int b)
{
if(a>b)
return b;
else
return a;
}
/*int log2(int n)
{
if(n==1)
return 0;
else
return(log2(n/2));
}*/
int decide(int cur,int index,bool max_dec,int weight[],int height)
{
int num;
//If we reach a leaf node
if(cur==height)
return weight[index];
//If the node is a max one we find the max from sub-nodes
if(max_dec)
num=max(decide(cur+1,index*2,false,weight,height),decide(cur+1,index*2+1,false,weight,height));
//If it is a min node we minimize the value under the sub-tree
else
num=min(decide(cur+1,index*2,true,weight,height),decide(cur+1,index*2+1,true,weight,height));
return num;
}
int main()
{
int scor[] = {3, 15, 2, 10, 12, 5, 2, 23};
int n= 8;
int h= log2(n);
int a= decide(0,0,true,scor,h);
cout<<a;
return 0;
}12
Complexity Analysis
Time complexity=O(h*m)
Where
h=height/depth of the tree generated
m=number of moves at each point
Thus was an introduction to the minimax algorithm and how it works!
Check out a few other posts