Sieve of Eratosthenes

Sieve of Eratosthenes is an algorithm in which we find out the prime numbers less than N. Here N is an integer value. This is an efficient method to find out the prime numbers to a limit. By using this we can find out the prime numbers till 10000000. Here the basic approach is used we just make a memory of size N-1. Store the value continuously from 2 to N in the memory. Now, we traverse from the first unmark number in the memory which is 2. Then, we mark all the multiples of 2 till N. Now we move to the next unmark number in the memory which is 3. Now we mark all the multiples of 3 which are unmarked. Repeat this process until we reach sqrt(N). Here now the unmarked number of our prime number. So, we just iterate one more time and store them in the answer. Let’s see how Sieve of Eratosthenes works.

Working Using Example

Step:1

Create a memory wich containing numbers from 2 to N(Here we take 100).

Step:2

Mark all the multiples of the first unmark number in the memory which is 2.

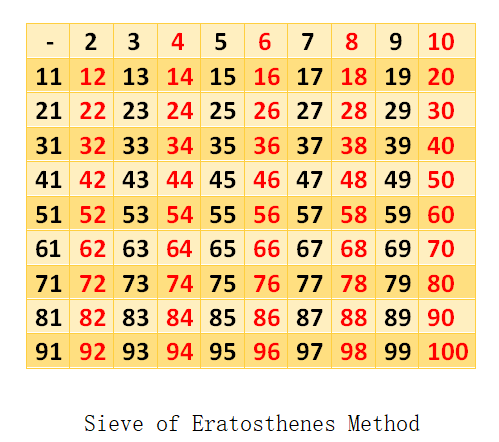
Step:3

Now mark all the multiples next unmarked number which is 3 in the memory.

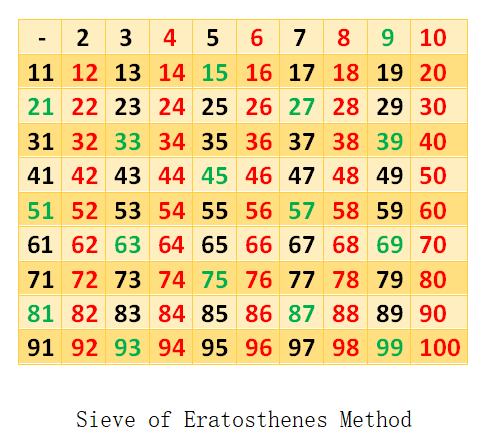
Step:4

Move to the next unmark number which is 5. Now mark all the multiples of 5.

Step:5

Move to the next unmarked number which is our last unmarked number in range 2 to the square root of N.

Step:6

All the remaining unmarked numbers are our prime numbers.

Prime Numbers: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 41, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

Algorithm

Step:1 Store the number from 2 to N in the list.
Step:2 Set all numbers as unmarked.
Step:3 For i in range 2 to Sqrt(N):
       If i is unmarked then:
          Marked all the multiples of i.
Step:4 Print all the unmarked numbers.

Implementation

/*C++ Implementation for Sieve of Eratosthenes.*/ 
#include<bits/stdc++.h>
using namespace std;
bool marked[1000000];
void Sieve(int n)
{
    /*for i from 2 to sqrt(N)*/
    for(int i=2;i*i<=n;i++) 
    {
        /*if i is unmarked*/
        if(marked[i]==false) 
        {  
            /*marked all the multiples of i*/
            for(int j=i*i;j<=n;j+=i) 
            {
                /*marked*/
                marked[j] = true; 
            }
        } 
    }
    cout<<"Prime number from 2 to N are: "<<endl;
    for(int i=2;i<=n;i++) 
    {
       if(marked[i]==false) 
       {
          cout<<i<<" "; 
       }
    }
    cout<<endl;
}
int main() 
{ 
    /*Take input N*/
    int n;
    cin>>n;
    /*call the sieve function*/
    Sieve(n);
    return 0; 
}

100

Prime number from 2 to N are: 
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 

Time Complexity

O(N*log(logN)) where N is the limit until we have to find the prime numbers. Here loglogN comes because of the loop run in the following pattern.

For 2 -> It runs N/2 times, For 3 -> It runs N/3 times, For 5 -> It runs N/5 times…

So, N*( 1/2 + 1/3 + 1/5 + 1/7 +……) = N*log(logN).

Note: Harmonic Progression of the sum of primes is equal to the log(logN) where N is the number of terms.

Space Complexity

O(N) where N is the limit until we have to find the prime numbers. We use this space to store the numbers which we use to mark.

References