Strongly Connected Components are the connected components of a given graph. SCC(strongly connected component) are those connected components in which every pair of a node have a path to visit from one to another node. SCC applied to Directed Graphs only.
This means the path between two nodes is a directed path not only a simple path. Let’s understand SCC of a directed graph by an example:
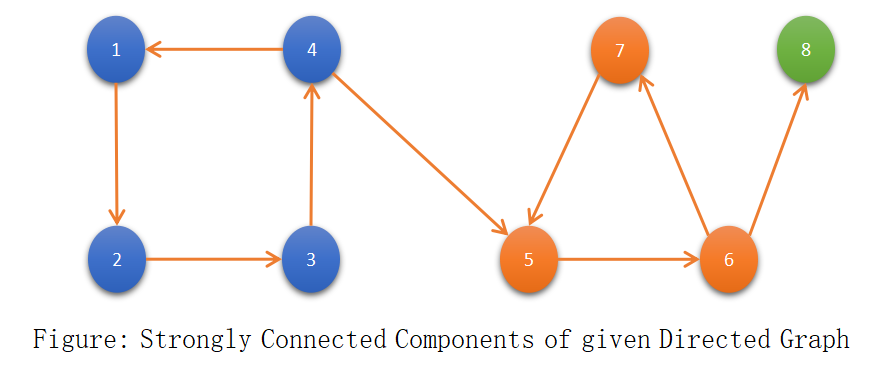
There are 3 strongly connected components (1,2,3,4), (5,6,7), (8).
Note: We can find the strongly connected component of a graph using Kosaraju’s algorithm. This is a linear time complexity algorithm.
Table of Contents
Working of Kosaraju’s Algorithm
Step:1 Apply DFS at the source node and store the nodes in a stack when the DFS is finished at that vertex. By following this we store the vertex of a graph in topological sorting. Top of Stack containing the vector which has maximum finishing time of DFS. We store the nodes in increasing order of finishing time.
Step:2 Change the direction of every edges to reverse the given graph.
Step:3 Now, apply DFS again on the current graph such that we always choose top of the stack as a source at which our DFS starts. When DFS completed then print all the visited vertex by current DFS because they are vertexes of SCC. Now, remove the node from the top of the stack. Apply DFS till we visit all the vertex of a graph by using the top of the stack as a source.
Algorithm For Strongly Connected Component
Step:1 Apply DFS(start) on the graph and store the finishing time of each node.
DFS(start):
i) visited[start]=true.
ii) for all neighbours u of start that are unvisited: DFS(u).
iii) stack.push(u).
Step:2 Reverse the graph.
i) Clear the adjacency list.
ii) for all edges between u to v: adjacency_list[v].push_back(u).
Step:3 Apply DFS from the vertex which is on the top of the stack.
While(!stack.empty()):
i) top=stack.top().
ii) stack.pop().
DFS(u).
iii) if the top is unvisited:
DFS(top).
Step:4 When all nodes which are visited will form SCC.
Step:5 Repeat till we get a vertex from the top of the stack which is unvisited.Implementation For Strongly Connected Component
/*C++ Implementation for finding Strongly Connected Components of a graph.*/
#include<bits/stdc++.h>
using namespace std;
void finishing_time(int v, vector<int> graph[],int visited[],stack<int> &s)
{
visited[v]=1;
for(int i=0;i<graph[v].size();i++)
{
if(!visited[graph[v][i]])
{
finishing_time(graph[v][i],graph,visited,s);
}
}
s.push(v);
}
void dfs(int source, vector<int> revrse_graph[],int visited[])
{
visited[source]=1;
cout<<source<<" ";
for(int i=0;i<revrse_graph[source].size();i++)
{
if(!visited[revrse_graph[source][i]])
{
dfs(revrse_graph[source][i],revrse_graph,visited);
}
}
}
int main()
{
/*Input the number of nodes, edges*/
int nodes,edges;
cin>>nodes>>edges;
vector<int> graph[nodes+1];
/*reverse of graph*/
vector<int> revrse_graph[nodes+1];
/*make graph*/
for(int i=0;i<edges;i++)
{
int x,y;
cin>>x>>y;
/*its directed graph so we add only edge for x->y*/
graph[x].push_back(y);
revrse_graph[y].push_back(x);
}
int visited[nodes+1];
/*set all nodes as unvisited(0)*/
memset(visited,0,sizeof(visited));
/*push the nodes in stack such that top of stack always more finishing time*/
stack<int> s;
/*push into stack*/
for(int i=1;i<=nodes;i++)
{
if(!visited[i])
{
finishing_time(i,graph,visited,s);
}
}
/*now, mark all the vertices as unvisited*/
memset(visited,0,sizeof(visited));
/*find the connected components*/
cout<<"strongly connected components of given directed graphs are: "<<endl;
while(s.size()>0)
{
/*pop the verte which is on the top of stack*/
int top=s.top();
s.pop();
/*if top is unvisited then apply DFS start from source vertex(top as source vertex)*/
if(!visited[top])
{
dfs(top,revrse_graph,visited);
cout<<endl;
}
}
return 0;
}8 9 1 2 2 3 3 4 4 1 4 5 5 6 6 7 7 5 6 8
strongly connected components of given directed graphs are: 1 4 3 2 5 7 6 8
Time Complexity
O(N+E) where N is the number of nodes and E is the number of edges. Means Kosaraju’s algorithm is a linear time complexity algorithm. By the use of DFS, we find the SCC and time complexity of DFS we already know which is O(N).
Space Complexity
O(N+E) where N denotes the number of nodes and E denotes the number of edges. While we create a graph using the adjacency list then that time memory space used is O(N+E).