Sliding Window Technique

Before getting on and along with what is the sliding window technique? What it does and how it does what it does let us get the hang of this concept by a small problem

Given an array of integers, we have the task of finding the minimum sum from all subarrays of size k.

Input: {1,4,0,3,5,2,6,1}

k=4

Output: Minimum sum sub-array of size 4 is (0,3)

Approach-1

Brute Force

Let us try to find the minimum sum from all subarrays by taking into account sums of k elements from index 0 to n-k+1.

Get all possible consecutive sub-arrays and then try to find the minimum sum from all of them.

Let us try to understand it with a code snippet.

Java Code for Sliding Window Technique

import java.util.*;
public class brute
{
  public static int maxk(int nums[],int k)
  {
    int min=Integer.MAX_VALUE;
    for(int i=0;i<nums.length-k+1;i++)
    {
      int sum=0;
      for(int j=i;j<i+k;j++)
      {
        sum=sum+nums[j];
      }
      min=Math.min(min,sum);
    }
    return min;
  }
  public static void main(String args[])
  {
    int a[]={1,4,0,3,5,2,6,1};
    int k=4;
    int ans=maxk(a,k);
    System.out.println(ans);
  }
}

C++ Code For Sliding Window Technique

#include<iostream>
using namespace std;
int mins(int a,int b)
{
  if(a>b)
    return b;
  else
    return a;
}
int maxk(int nums[],int k,int l)
{
  int min=9999;
  for(int i=0;i<l-k+1;i++)
  {
    int sum=0;
    for(int j=i;j<i+k;j++)
    {
      sum=sum+nums[j];
    }
    min=mins(min,sum);
  }
  return min;
}
int main()
{
  int a[]={1,4,0,3,5,2,6,1};
  int k=4;
  int l=sizeof(a)/sizeof(a[0]);
  int ans=maxk(a,k,l);
  cout<<ans;
}

{1,4,0,3,5,2,6,1}
4

(0,3)

Complexity Analysis for Sliding Window Technique

Time Complexity for the above approach=O(n^2)

However, in this era of the fast and the furious who wants an O(n^2) solution.

We definitely need to optimize it. What shall we do?

I recommend a new technique.

What is the sliding window?

This concept feels/is like a caterpillar trying to climb up a tree.

What is the window?

The window is a sequence part of the array that moves through it

Not clear enough?

Here is an illustration to clarify it

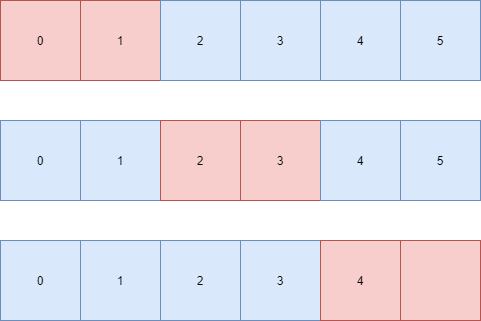
In the above figure the red region(window) of size 2 slides through the array.

If we take I as the starting and j as the ending index of the window as we move through the array both of them increment by one to give us a sliding window of size 2.

Let us now solve the same problem “Sliding Window Technique” with the new concept we have

Approach-2

Sliding Window

• Calculate the sum of first k numbers and put it in sum

TADA! our first window’s sum is done

• Find the sum in each window by
  • Removing stale data from last window i.e array[current_start-1]
  • Adding fresh data i.e array[previous_end+1]
  • Thus, sliding the window
• We find the minimum of the sum from all the windows

Voila! We are now able to solve the same problem in O(n) time

Java Code for Sliding Window Technique

import java.util.*;
public class brute
{
  public static int maxk(int nums[],int k,int n)
  {
    //If the array does not contain k elements it is not eligible
    if(n<k)
      return -1;
    //Declaring the minimum
    int min=0;
    //Finding the sum of first k elements
    for(int i=0;i<k;i++)
      min=min+nums[i];
    int cur=min;
    //As the sliding window moves 
    //We move the start and end index by 1
    for(int i=k;i<n;i++)
    {
      //Thus we remove the initial index value
      cur=cur-nums[i-k]+nums[i];
      //And add the current index value
      min=Math.min(cur,min);
    }
    return min;
  }
  public static void main(String args[])
  {
    int a[]={1,1,0,3,2,2,6,1};
    int k=5;
    int n=a.length;
    int ans=maxk(a,k,n);
    System.out.println(ans);
  }
}

C++ Code for Sliding Window Technique

#include<iostream>
using namespace std;
    int mins(int a,int b)
    {
    	if(a>b)
    		return b;
    	else
    		return a;
    }
    int maxk(int nums[],int k,int n)
  {
    //If the array does not contain k elements it is not eligible
    if(n<k)
      return -1;
    //Declaring the minimum
    int min=0;
    int i=0;
    //Finding the sum of first k elements
    for(i=0;i<k;i++)
      min=min+nums[i];
    int cur=min;
    //As the sliding window moves 
    //We move the start and end index by 1
    for(i=k;i<n;i++)
    {
      //Thus we remove the initial index value
      cur=cur-nums[i-k]+nums[i];
      //And add the current index value
      min=mins(cur,min);
    }
    return min;
  }
  int main()
  {
    int a[]={1,1,0,3,2,2,6,1};
    int k=5;
    int n=8;
    int ans=maxk(a,k,n);
    cout<<ans;
  }

{1,1,0,3,2,2,6,1}
5

(0,4)

Complexity Analysis

Time complexity=O(n)

Here you have it with you. The fixed sliding window concept explained!

How about practicing with the newly acquired knowledge of a problem?

References