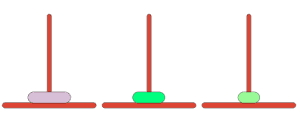
Tower Of Hanoi

Tower of Hanoi is a mathematical problem with the following conditions:

• There are three towers
• There may be n number of rings present
• The rings are of different sizes
• Only one disk can be moved at a time
• Any disk can only be moved on the top of a bigger disk
• Only the top disk can be removed

Explanation

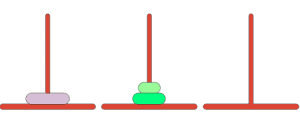
Let us look at how this problem can be handled when we have two disks

We move the top(small) disk onto the next tower after which we move the second disk to the third tower and then eventually shift the first disk as well on to the third tower. (3 moves)

Assumption: The disks are initially sorted

Similarly when we work with 3 disks. We would need 7 steps to shift all of them to the third ring.

• Disk 1 moved from 1 to 3
• Now, Disk 2 moved from 1 to 2
• Disk 1 moved from 3 to 2
• Disk 3 moved from 1 to 3
• Now, Disk 1 moved from 2 to 1
• Disk 2 moved from 2 to 3
• Disk 1 moved from 1 to 3

We are thus moving n-1 disks on to the second tower, the last disk to the third tower and n-1 disks onto the first disk thus completing the shift.

Let us now look at a recursive implementation of the same.

JAVA Program for Tower Of Hanoi

public class hanoi
{
  public static void hanoi(int n,char from,char mid,char to)
  {
    if(n==1)
    {
      //Moving disk1 on to the first rod
      System.out.println("Moving disk "+n+"From rod:"+from+"To Rod"+to);
      return;
    }
    //Moving n-1 disks to the second rod
    hanoi(n-1,from,to,mid);
    System.out.println("Moving disk "+n+"From rod:"+from+"To Rod"+to);
    //Moving the disks on top of already moved first disk
    hanoi(n-1,mid,from,to);
  }
  public static void main(String args[])
  {
    int n=3;
    hanoi(n,'A','B','C');
  }
}

C++ Program for Tower Of Hanoi

#include<iostream>
using namespace std;
  void hanoi(int n,char from,char mid,char to)
  {
    if(n==1)
    {
      //Moving disk1 on to the first rod
      cout<<"Moving disk "<< n <<"From rod:"<< from <<" To Rod:"<< to <<endl;
      return;
    }
    //Moving n-1 disks to the second rod
    hanoi(n-1,from,to,mid);
    cout<<"Moving disk "<< n <<"From rod:"<< from <<" To Rod:"<< to <<endl;
    //Moving the disks on top of already moved first disk
    hanoi(n-1,mid,from,to);
  }
  int main()
  {
    int n=4;
    hanoi(n,'A','B','C');
  }

Moving disk 1From rod: A To Rod: B
Moving disk 2From rod:A To Rod:C
Moving disk 1From rod:B To Rod:C
Moving disk 3From rod: A To Rod: B
Moving disk 1From rod:C To Rod:A
Moving disk 2From rod:C To Rod:B
Moving disk 1From rod: A To Rod: B
Moving disk 4From rod:A To Rod:C
Moving disk 1From rod:B To Rod:C
Moving disk 2From rod: B To Rod: A
Moving disk 1From rod:C To Rod:A
Moving disk 3From rod:B To Rod:C
Moving disk 1From rod: A To Rod: B
Moving disk 2From rod:A To Rod:C
Moving disk 1From rod:B To Rod:C

Conclusion for Tower Of Hanoi

We thus come to the conclusion:

15 moves for 4 disks

31 moves for 5 disks

Thus, we come to the conclusion that for n disks we need to make (2^n)-1 moves.

2 disks=(2*2)-1=2 moves

3 disks=(2^3)-1=7 moves

4 disks=(2^4)-1=15 moves

and so on.

Complexity Analysis for Tower Of Hanoi

Time Complexity

Recursive Equation: 

, or you can say  which is exponential

Space Complexity

T(n) = T(n-1) + k
T(0) = k
T(1) = 2k
T(2) = 3k
T(3) = 4k
So the space complexity is O(n).

References