Given a strictly increasing array of positive integers, find the length of the longest fibonacci subsequence.
A sequence of n elements is fibonacci like if,
- n >= 3
- xi = x(i – 2) + x(i -1), where xi is the ith term of the sequence and i >= 2
Table of Contents
Examples
Input
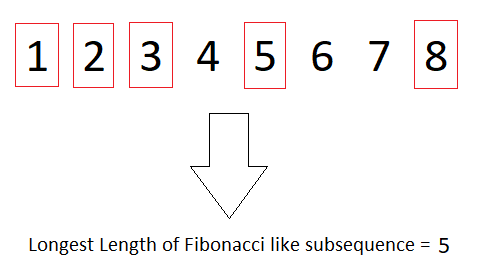
arr[] = {1, 2, 3, 4, 5, 6, 7, 8}
Output
5
Explanation
The longest fibonacci like subsequence is {1, 2, 3, 5, 8}
Input
arr[] = {1, 3, 7, 11, 12, 14, 18}
Output
3
Explanation
The longest fibonacci like subsequence is {1, 11, 12} or {3, 11, 14} or {7, 11, 18}
Naive Approach for the length of longest fibonacci subsequence
For a fibonacci like sequence, the first two terms can attain any value and the remaining terms are determined by using the formula mentioned above. For Example,
If the first term be 2 and second term be 3, the fibonacci like sequence looks like 2, 3, 5, 8, 11,….
The algorithm is to choose any two elements as the first and second term of the Fibonacci like sequence, let these be represented as arr[i] and arr[j] respectively. Then the next term will be (arr[i] + arr[j]), search for the next term in the array. If it exists then the next term will become (arr[j] + (arr[i] + arr[j])), again search for the next term and repeat this process till the next term continues to exist in the array and find the maximum length of fibonacci like sequence.
The searching for next term in the array can be optimized using hashing.
Complexity Analysis for the length of longest fibonacci subsequence
Time Complexity = O(n2 * log(m))
Space Complexity = O(n)
where n is the number of elements in the given array and m is the maximum value in the given array.
JAVA Code
import java.util.HashSet;
public class LengthOfLongestFibonacciSubsequence {
private static int longestLengthFibonacci(int[] arr) {
int n = arr.length;
HashSet<Integer> set = new HashSet<>();
// Store all the elements of array in a hash set
for (int i = 0; i < n; i++) {
set.add(arr[i]);
}
int maxLength = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
// Choose any two elements as the first and second term of fibonacci like sequence
int firstTerm = arr[i];
int secondTerm = arr[j];
int nextTerm = firstTerm + secondTerm;
int currLength = 2;
// Search for next term till it exists in the array
while (set.contains(nextTerm)) {
currLength++;
firstTerm = secondTerm;
secondTerm = nextTerm;
// Update next term
nextTerm = firstTerm + secondTerm;
}
// Update the maximum length of fibonacci like sequence
maxLength = Math.max(maxLength, currLength);
}
}
// If maxLength is 2, then return 0, else return maxLength
return (maxLength == 2) ? 0 : maxLength;
}
public static void main(String[] args) {
// Example 1
int arr1[] = new int[] {1, 2, 3, 4, 5, 6, 7, 8};
System.out.println(longestLengthFibonacci(arr1));
// Example 2
int arr2[] = new int[] {1, 3, 7, 11, 12, 14, 18};
System.out.println(longestLengthFibonacci(arr2));
}
}5 3
C++ Code
#include<bits/stdc++.h>
using namespace std;
int longestLengthFibonacci(int *arr, int n) {
set<int> hashSet;
// Store all the elements of array in a hash set
for (int i = 0; i < n; i++) {
hashSet.insert(arr[i]);
}
int maxLength = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
// Choose any two elements as the first and second term of fibonacci like sequence
int firstTerm = arr[i];
int secondTerm = arr[j];
int nextTerm = firstTerm + secondTerm;
int currLength = 2;
// Search for next term till it exists in the array
while (hashSet.find(nextTerm) != hashSet.end()) {
currLength++;
firstTerm = secondTerm;
secondTerm = nextTerm;
// Update next term
nextTerm = firstTerm + secondTerm;
}
// Update the maximum length of fibonacci like sequence
maxLength = std::max(maxLength, currLength);
}
}
// If maxLength is 2, then return 0, else return maxLength
return (maxLength == 2) ? 0 : maxLength;
}
int main() {
// Example 1
int arr1[] = {1, 2, 3, 4, 5, 6, 7, 8};
cout<<longestLengthFibonacci(arr1, sizeof(arr1) / sizeof(arr1[0]))<<endl;
// Example 2
int arr2[] = {1, 3, 7, 11, 12, 14, 18};
cout<<longestLengthFibonacci(arr2, sizeof(arr2) / sizeof(arr2[0]))<<endl;
return 0;
}5 3
Optimal Approach for the length of longest fibonacci subsequence
The above problem can be solved optimally using dynamic programming.
Any two terms can form the first two terms of the Fibonacci like sequence, create a 2-D array dp of size (n X n), where n is the size of the array. An element of the 2-D array, dp[i][j], denotes the maximum length of the Fibonacci sequence ending at (i, j), that is, the last two terms of the sequence are i and j respectively.
Consider an example, arr[] = {1, 2, 3, 4, 5, 6, 7, 8}
One possible fibonacci like sequence is {1, 2, 3, 5, 8}, that is, {arr[0], arr[1], arr[2], arr[4], arr[7]}
Initially the length of longest fibonacci sequence ending at any (i, j) is 2, that is, dp[i][j] = 2 initially.
The maximum length of sequence ending at (j, k) = 1 + maximum length of sequence ending at (i, j), where i is the index of element(arr[k] – arr[j]).
That is,
dp[j][k] = 1 + dp[i][j], where i is the index of element (arr[k] – arr[j]) in array arr.
- Store the index of all the elements of array arr in a hash map.
- Create a 2-D array dp of size (n X n), where n is the length of array arr.
- The initial value of all the elements of array dp is 2.
- For every pair (j, k), where k > j, calculate the index i as described above, if i exists and is different from j, update dp[j][k] as (1 + dp[i][j]). Also update the maximum length of fibonacci like sequence.
- If the maximum length of fibonacci like sequence is 2, return 0, else return the maximum length.
Complexity Analysis for the length of longest fibonacci subsequence
Time Complexity = O(n2)
Space Complexity = O(n2)
where n is the number of elements in the given array.
JAVA Code
import java.util.HashMap;
public class LengthOfLongestFibonacciSubsequence {
private static int longestLengthFibonacci(int[] arr) {
int n = arr.length;
// Store the indices of all the elements of arr
HashMap<Integer, Integer> index = new HashMap<>();
for (int i = 0; i < n; i++) {
index.put(arr[i], i);
}
// Initialize all the elements of dp as 2
int dp[][] = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j] = 2;
}
}
int maxLength= 2;
for (int k = 0; k < n; k++) {
for (int j = 0; j < k; j++) {
// For every pair (j, k)
if (index.containsKey(arr[k] - arr[j])) {
// Find the index i
int i = index.get(arr[k] - arr[j]);
// if i and j are not same
if (i != j) {
// use the formula dp[j][k] = 1 + dp[i][j]
dp[j][k] = 1 + dp[i][j];
// Update the maximum length
maxLength = Math.max(maxLength, dp[j][k]);
}
}
}
}
// If maxLength is 2, then return 0, else return maxLength
return (maxLength == 2) ? 0 : maxLength;
}
public static void main(String[] args) {
// Example 1
int arr1[] = new int[] {1, 2, 3, 4, 5, 6, 7, 8};
System.out.println(longestLengthFibonacci(arr1));
// Example 2
int arr2[] = new int[] {1, 3, 7, 11, 12, 14, 18};
System.out.println(longestLengthFibonacci(arr2));
}
}5 3
C++ Code
#include<bits/stdc++.h>
using namespace std;
int longestLengthFibonacci(int *arr, int n) {
// Store the indices of all the elements of arr
unordered_map<int, int> index;
for (int i = 0; i < n; i++) {
index.insert(make_pair(arr[i], i));
}
// Initialize all the elements of dp as 2
int dp[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j] = 2;
}
}
int maxLength = 2;
for (int k = 0; k < n; k++) {
for (int j = 0; j < k; j++) {
// For every pair (j, k)
auto itr = index.find(arr[k] - arr[j]);
if (itr != index.end()) {
// Find the index i
int i = itr->second;
// if i and j are not same
if (i != j) {
// use the formula dp[j][k] = 1 + dp[i][j]
dp[j][k] = 1 + dp[i][j];
// Update the maximum length
maxLength = std::max(maxLength, dp[j][k]);
}
}
}
}
// If maxLength is 2, then return 0, else return maxLength
return (maxLength == 2) ? 0 : maxLength;
}
int main() {
// Example 1
int arr1[] = {1, 2, 3, 4, 5, 6, 7, 8};
cout<<longestLengthFibonacci(arr1, sizeof(arr1) / sizeof(arr1[0]))<<endl;
// Example 2
int arr2[] = {1, 3, 7, 11, 12, 14, 18};
cout<<longestLengthFibonacci(arr2, sizeof(arr2) / sizeof(arr2[0]))<<endl;
return 0;
}5 3