Longest Common Prefix Using Word by Word Matching

Given a list of words, find the longest common prefix of all the words by word by word matching.

Examples

Input:
list[] = {“apple”, “ape”, “april”}
Output:
ap
Input:
list[] = {“star”, “stole”, “steam”, “start”}
Output:
st

Algorithm for Longest Common Prefix

The longest common prefix of two words is found as,
Let W1 be the first word and W2 be the second word,

1. Initialize a string variable commonPrefix as “”(empty string).
2. Start traversing in W1 and W2 simultaneously, till we reach the end of any one of the words.
3. Match the characters of W1 and W2, if these are equal append it to commonPrefix and advance in both the words.
4. Else return commonPrefix

The above algorithm can be extended to find the longest common prefix of list of N words as,

1. Initialize a string variable commonPrefix as first word in the list.
2. Traverse in the list starting from index 1(o based indexing).
3. Update commonPrefix as a common prefix of commonPrefix and current word in the list.
4. At the end of the traversal return commonPrefix.

Explanation for Longest Common Prefix

Consider an example,
list[] = {“star”, “stole”, “steam”, “start”}

Step 1
commonPrefix = “star”

Step 2
Repeat step 3 and 4 while traversing the list from index 1 to end of the list.

Step 3 and 4
Iteration 1
commonPrefix= common prefix of (commonPrefix, “stole”)
commonPrefix = “st”
Iteration 2
commonPrefix= common prefix of (commonPrefix, “steam”)
commonPrefix = “st”
Iteration 3
commonPrefix = common prefix of (commonPrefix, “start”)
commonPrefix = “st”

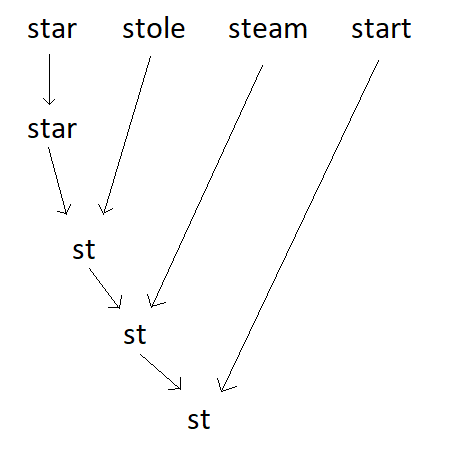
We have traversed the list and the common prefix of all the words in the list is “st”. See the image below for clarification.

JAVA Code

public class LongestCommonPrefixUsingWordByWordMatching {
    // Function to find common prefix of two words
    private static String prefix(String W1, String W2) {
        // Initialize prefix as empty string
        String prefix = "";

        int n1 = W1.length();
        int n2 = W2.length();
        int i = 0, j = 0;

        // Traverse in W1 and W2 simultaneously
        while (i < n1 && j < n2) {
            // If characters of W1 and W2 are equal, append it to answer else return prefix
            if (W1.charAt(i) == W2.charAt(j)) {
                prefix += W1.charAt(i);
                i++;
                j++;
            } else {
                return prefix;
            }
        }

        // All words matched, return prefix
        return prefix;
    }

    private static String longestCommonPrefix(String[] list) {
        // Initialize longest common prefix as first word of list
        String lcp = list[0];
        
        // Traverse the list from index 1 (0 based indexing)
        for (int i = 1; i < list.length; i++) {
            // Update lcp as prefix of lcp and current word
            lcp = prefix(list[i], lcp);
        }
        
        // return lcp
        return lcp;
    }

    public static void main(String[] args) {
        // Example 1
        String list1[] = new String[] {"apple", "ape", "april"};
        System.out.println(longestCommonPrefix(list1));

        // Example 2
        String list2[] = new String[] {"star", "stole", "steam", "start"};
        System.out.println(longestCommonPrefix(list2));
    }
}

C++ Code for Longest Common Prefix

#include <bits/stdc++.h>
using namespace std;

// Function to find common prefix of two words
string prefix(string W1, string W2) {
    // Initialize prefix as empty string
    string prefix = "";
    
    int n1 = W1.size();
    int n2 = W2.size();
    int i = 0, j = 0;
    
    // Traverse in W1 and W2 simultaneously
    while (i < n1 && j < n2) {
        // If characters of W1 and W2 are equal, append it to answer else return prefix
        if (W1[i] == W2[j]) {
            prefix += W1[i];
            i++;
            j++;
        } else {
            return prefix;
        }
    }

    // All words matched, return prefix
    return prefix;
}

string commonPrefix(vector<std::string> &list) {
    // Initialize longest common prefix as first word of list
    string lps = list.front();
    
    // Traverse the list from index 1 (0 based indexing)
    for (auto itr = list.begin() + 1; itr != list.end(); itr++) {
        // Update lcp as prefix of lcp and current word
        lps = prefix(lps, *itr);
    }
    
    // return lcp
    return lps;
}

int main() {
    // Example 1
    vector<std::string> list1;
    list1.push_back("apple");
    list1.push_back("ape");
    list1.push_back("april");
    cout<<commonPrefix(list1)<<endl;
    
    // Example 2
    vector<std::string> list2;
    list2.push_back("star");
    list2.push_back("stole");
    list2.push_back("steam");
    list2.push_back("start");
    cout<<commonPrefix(list2)<<endl;
    
    return 0;
}

ap
st

Complexity Analysis for Longest Common Prefix

Time Complexity = O(N * maximum length of a word in the list) 
Space Complexity = O(1)
where N is the total number of words in the list.

References