In sorting a queue without extra space problem we have given a queue, sort it using standard queue operations without extra space.
Table of Contents
Examples
Input
queue = 10 -> 7 -> 2 -> 8 -> 6
Output
queue = 2 -> 6 -> 7 -> 8 -> 10
Input
queue = 56 -> 66 -> 1 -> 18 -> 23 -> 39
Output
queue = 1 -> 18 -> 23 -> 39 ->56 -> 66
Input
queue = 5 -> 4 -> 3 -> 2 -> 1
Output
queue = 1 -> 2 -> 3 -> 4 -> 5
Algorithm for Sorting a Queue without Extra Space
Consider the queue made up of two parts, one is sorted and the other is not sorted. Initially, all the elements are present in not sorted part.
At every step, find the index of the minimum element from the unsorted queue and move it to the end of the queue, that is, to the sorted part.
Repeat this step till all the elements are not present in the sorted queue.
- Run a loop for i = 0 to n(not included), where n is the size of the queue.
- At every iteration initialize minIndex as -1 and minValue as -infinity.
- Run another loop with variable j that finds the minimum element’s index from the unsorted queue. The unsorted queue is present from index 0 to index (n – i) for a particular value of i. At every iteration, if the current element is less than minValue, update minValue as current element and minIndex as j.
- Traverse in the queue and remove the element at position minIndex and push it at the end of the queue.
- The queue is sorted, print its elements.
Explanation for Sorting a Queue without Extra Space
Consider an example,
queue = 10 -> 7 -> 2 -> 8 -> 6
Initially, all the elements are present in the unsorted part, that is,

At every step, find the index of minimum element in the unsorted part and move it to the end of the queue, that is, sorted part.
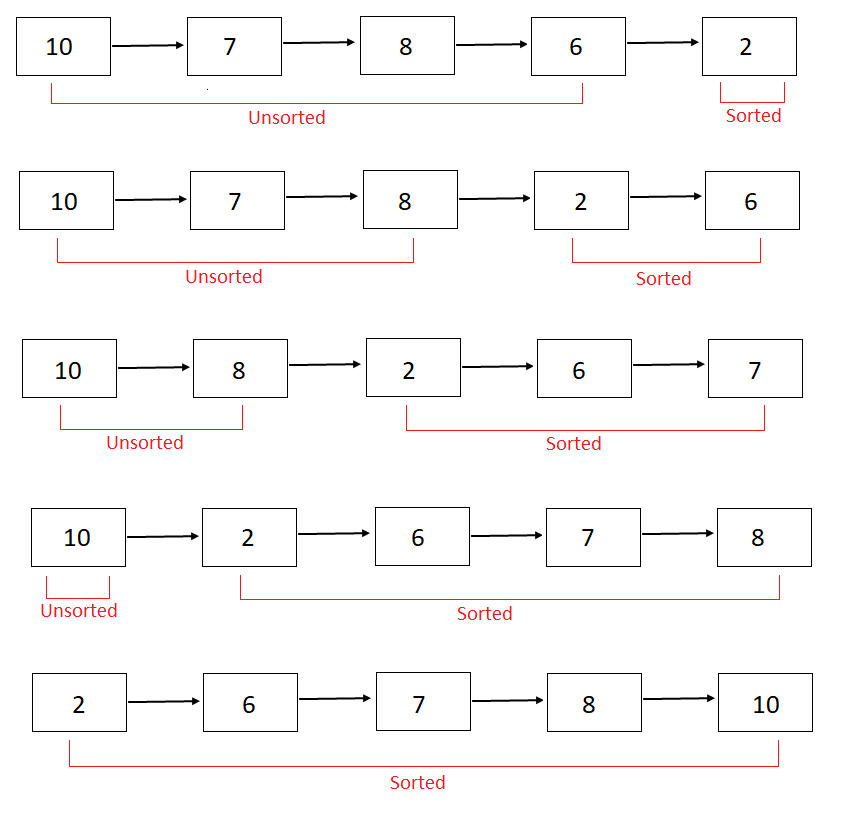
All the elements are present in sorted part, so we stop.
JAVA Code for Sorting a Queue without Extra Space
import java.util.LinkedList;
import java.util.Queue;
public class SortingAQueueWithoutExtraSpace {
private static void sortQueue(Queue<Integer> queue) {
int n = queue.size();
for (int i = 0; i < n; i++) {
// Find the index of smallest element from the unsorted queue
int minIndex = -1;
int minValue = Integer.MAX_VALUE;
for (int j = 0; j < n; j++) {
int currValue = queue.poll();
// Find the minimum value index only from unsorted queue
if (currValue < minValue && j < (n - i)) {
minValue = currValue;
minIndex = j;
}
queue.add(currValue);
}
// Remove min value from queue
for (int j = 0; j < n; j++) {
int currValue = queue.poll();
if (j != minIndex) {
queue.add(currValue);
}
}
// Add min value to the end of the queue
queue.add(minValue);
}
// Print the sorted queue
for (Integer i : queue) {
System.out.print(i + " ");
}
System.out.println();
}
public static void main(String[] args) {
// Example 1
Queue<Integer> q1 = new LinkedList<>();
q1.add(10);
q1.add(7);
q1.add(2);
q1.add(8);
q1.add(6);
sortQueue(q1);
// Example 2
Queue<Integer> q2 = new LinkedList<>();
q2.add(56);
q2.add(66);
q2.add(1);
q2.add(18);
q2.add(23);
q2.add(39);
sortQueue(q2);
}
}2 6 7 8 10 1 18 23 39 56 66
C++ Code for Sorting a Queue without Extra Space
#include<bits/stdc++.h>
using namespace std;
void sortQueue(queue<int> &queue) {
int n = queue.size();
for (int i = 0; i < n; i++) {
// Find the index of smallest element from the unsorted queue
int minIndex = -1;
int minValue = INT_MAX;
for (int j = 0; j < n; j++) {
int currValue = queue.front();
queue.pop();
// Find the minimum value index only from unsorted queue
if (currValue < minValue && j < (n - i)) {
minValue = currValue;
minIndex = j;
}
queue.push(currValue);
}Nvidia
Belzabar
// Remove min value from queue
for (int j = 0; j < n; j++) {
int currValue = queue.front();
queue.pop();
if (j != minIndex) {
queue.push(currValue);
}
}
// Add min value to the end of the queue
queue.push(minValue);
}
// Print the sorted queue
for (int i = 0; i < n; i++) {
int curr = queue.front();
queue.pop();
cout<<curr<<" ";
queue.push(curr);
}
cout<<endl;
}
int main() {
// Example 1
queue<int> q1;
q1.push(10);
q1.push(7);
q1.push(2);
q1.push(8);
q1.push(6);
sortQueue(q1);
// Example 2
queue<int> q2;
q2.push(56);
q2.push(66);
q2.push(1);
q2.push(18);
q2.push(23);
q2.push(39);
sortQueue(q2);
}2 6 7 8 10 1 18 23 39 56 66
Complexity Analysis
Time Complexity = O(n2)
Space Complexity = O(1)
where n is the number of elements in the queue.