In the Maximum Subarray problem we have given an integer array nums, find the contiguous sub array which has the largest sum and print the maximum sum subarray value.
Table of Contents
Example
Input
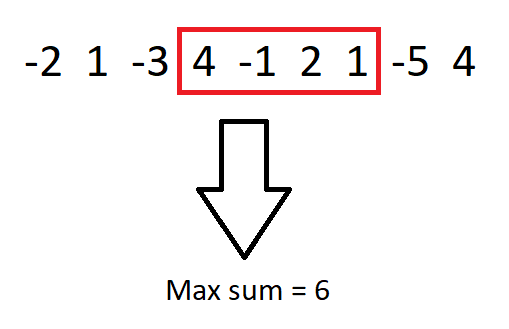
nums[] = {-2, 1, -3, 4, -1, 2, 1, -5, 4}
Output
6
Algorithm
The goal is to find the maximum sum in a line(contiguous sub-array) in the nums array, which is achieved using Kadane’s Algorithm.
We use two global variables, max and maxTillNow, where max stores the final answer, and maxTillNow stores the maximum result till the ith index.
Initialize max and maxTillNow as nums[0], run a loop from 1 to n, during each iteration maxTillNow becomes maximum of nums[i] and (maxTillNow + nums[i]) and max becomes maximum of max and maxTillNow.
Finally, we return max, which stores the maximum subarray sum.
Complexity Analysis
Time Complexity = O(n) where n is the number of integer present in the given array.
Space Complexity = O(1)
Explanation for Maximum Subarray
Consider the case where nums = {2, -1, 3, 5, -2, 1}
Initialize,
- max = nums[0] = 2 and maxTillNow = 2
- for i = 1, nums[i] = -1
maxTillNow = max(-1, -1 + 2) = max(-1, 1) = 1
max = max(2, 1) = 2 - for i = 2, nums[i] = 3 for i = 4, nums[i] = -2
- maxTillNow = max(-2, -2 + 9) = max(-2, 7) = 7
max = max(9, 7) = 9 - for i = 5, nums[i] = 1
maxTillNow = max(1, 1 + 7) = max(1, 8) = 8
max = max(9, 8) = 9 - Loop ends and we return max as 9, which is the answer. Here 9 is our maximum subarray sum.
Pseudo Code
- Intialize max and maxTillNow as nums[0]
- loop for (i = 1 to less than n)
- maxTillNow = maximum(maxTillNow + nums[i], nums[i])
- max = maximum(max, maxTillNow)
- end for
- return max
JAVA Code for Maximum Subarray
public class MaximumSubarray {
public static void main(String[] args) {
// Input array
int nums[] = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
// Find the maximum subarray using Kadane's algorithm
int maxSum = findMaxSubarray(nums);
// Print the answer
System.out.println(maxSum);
}
private static int findMaxSubarray(int[] nums) {
// Initialise max and maxTillNow as nums[0]
int max = nums[0];
int maxTillNow = nums[0];
// Loop through the array
for (int i = 1; i < nums.length; i++) {
// maxTillNow is max of curr element or maxTillNow + curr element
maxTillNow = Math.max(nums[i], maxTillNow + nums[i]);
// max is maximum of max and maxTillNow
max = Math.max(max, maxTillNow);
}
// Return the result
return max;
}
}
C++ Code for Maximum Subarray
#include <bits/stdc++.h>
using namespace std;
int findMaxSubarray(int *nums, int n) {
// Initialise max and maxTillNow as nums[0]
int max = nums[0];
int maxTillNow = nums[0];
// Loop through the array
for (int i = 1; i < n; i++) {
// maxTillNow is max of curr element or maxTillNow + curr element
maxTillNow = std::max(nums[i], maxTillNow + nums[i]);
// max is maximum of max and maxTillNow
max = std::max(max, maxTillNow);
}
// Return the result
return max;
}
int main() {
// Input array
int nums[] = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
int n = sizeof(nums) / sizeof(*nums);
// Find the maximum subarray using Kadane's algorithm
int maxSum = findMaxSubarray(nums, n);
// Print the answer
cout<<maxSum<<endl;
return 0;
}{-2, 1, -3, 4, -1, 2, 1, -5, 4}6