Check if any two intervals overlap among a given set of intervals

Difficulty Level Medium
Frequently asked in Amazon Arcesium Cisco Directi JP Morgan Microsoft Qualcomm Yandex
Dynamic Programming SortingViews 1843

Problem Statement

The problem “Check if any two intervals overlap among a given set of intervals” states that you are given some set of intervals. Each interval consists of two values, one is starting time and the other is ending time. The problem statement asks to check if any of the intervals overlap each other if overlaps then print ‘YES’ else print ‘NO’.

Example

arr[] = { { 2, 3 }, { 5, 6 }, { 1, 4 }, { 7, 9 }}
Yes

Explanation

Because, the time interval (2, 3) and (1, 4) overlaps with each other.

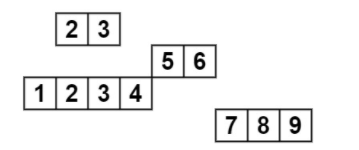
Check if any two intervals overlap among a given set of intervals

The image clearly depicts that intervals (2,3) and (1,4) overlap.

arr[] = { { 1, 4 }, { 5, 6 }, { 7, 9 }, { 10, 13 } }
No

Explanation

Because none of the intervals overlaps each other.

Algorithm

  1. Find the maximum ending value of an interval (maximum element).
  2. Create an array of size as same as the maximum element we found.
  3. Traverse the given input array, get the starting and ending value of each interval,
  4. Insert into the temp array and increase the value of starting time by 1, and decrease the value of (ending time + 1) by 1.
  5. Traverse the array up to the maximum element we found,
  6. Sum up the previous value and current value and store it into the temp array, check if any value is greater than 1, then return true.
  7. Return false.

Explanation

Our problem is to check if any two intervals overlap among a given set of intervals. So, we are given a set of intervals, each interval consists of two values, one is ending value and the other is starting value of a time interval. We have to determine if any of the intervals are overlapping. If any of the intervals are overlapping or covering the whole interval, then we have to print yes, else print no. For this, we are going to find out the maximum element of the time interval, since the ending time is always maximum, so we will be searching for the maximum element in the ending time interval, we always find the maximum value there.

After this create a temp array having the same size as of the given array value. Use this array to put the starting and ending time of the interval. But before that, we will get the values of starting time and ending time of the interval. Put the starting time and ending time of the interval into the temp and increasing the value of starting time by 1 and decrease the value of (ending time + 1) by 1 and updating the temp array.

We are going to traverse the temp array we created and update up to the maximum element we found at the start of the code. Then after we will do the addition of the current value and the previous value of the temp array, for each traversal check if any of the updated value has the value greater than 1, this will check if any of the overlappings occurs, if it is true, then return true. After all the traversing has been done, return false, if we come here in this line, means no overlapping occurs. So we will return false. If you wanna take a look, there’s a similar problem which asks us to merge overlapping intervals.

Code

C++ code to check interval overlapping

#include <algorithm>
#include <iostream>

using namespace std;

struct Input_Interval
{
    int start;
    int end;
};

bool overLappingCheck(Input_Interval arr[], int n)
{

    int maximumElement = 0;

    for (int i = 0; i < n; i++)
    {
        if (maximumElement < arr[i].end)
            maximumElement = arr[i].end;
    }

    int temp[maximumElement + 2] = { 0 };

    for (int i = 0; i < n; i++)
    {
        int startingTime = arr[i].start;

        int endingTime = arr[i].end;
        temp[startingTime]++, temp[endingTime + 1]--;
    }

    for (int i = 1; i <= maximumElement; i++)
    {
        temp[i] += temp[i - 1];

        if (temp[i] > 1)
            return true;
    }

    return false;
}

int main()
{
    Input_Interval arr1[] = { { 2, 3 }, { 5, 6 }, { 1, 4 }, { 7, 9 } };
    int n1 = sizeof(arr1) / sizeof(arr1[0]);

    overLappingCheck(arr1, n1) ? cout << "Yes\n" : cout << "No\n";

    Input_Interval arr2[] = { { 1, 4 }, { 5, 6 }, { 7, 9 }, { 10, 13 } };
    int n2 = sizeof(arr2) / sizeof(arr2[0]);
    overLappingCheck(arr2, n2) ? cout << "Yes\n" : cout << "No\n";

    return 0;
}

Yes
No

Java code to check interval overlapping

class IntervalOverLapping
{
    static class Input_Interval
    {
        int start;
        int end;
        public Input_Interval(int start, int end)
        {
            super();
            this.start = start;
            this.end = end;
        }
    };
    
    static boolean overLappingCheck(Input_Interval arr[], int n)
    {

        int maximumElement = 0;

        for (int i = 0; i < n; i++)
        {
            if (maximumElement < arr[i].end)
                maximumElement = arr[i].end;
        }
        
        int []temp = new int[maximumElement + 2];
        
        for (int i = 0; i < n; i++)
        {
            int startingTime = arr[i].start;

            int endingTime = arr[i].end;
            temp[startingTime]++;
            temp[endingTime+1]--;
        }
        
        for (int i = 1; i <= maximumElement; i++)
        {
            temp[i] += temp[i - 1];

            if (temp[i] > 1)
                return true;
        }
        
        return false;
    }
    
    public static void main(String[] args)
    {
        Input_Interval arr1[] = { new Input_Interval(2, 3), new Input_Interval(5, 6),
                           new Input_Interval(1, 4), new Input_Interval(7, 9)
        };
        int n1 = arr1.length;

        if(overLappingCheck(arr1, n1))
            System.out.print("Yes\n");
        else
            System.out.print("No\n");

        Input_Interval arr2[] = { new Input_Interval(1, 4), new Input_Interval(5, 6),
                           new Input_Interval(7, 9), new Input_Interval(10, 13)
        };

        int n2 = arr2.length;
        if(overLappingCheck(arr2, n2))
            System.out.print("Yes\n");
        else
            System.out.print("No\n");
    }
}

Yes
No

Complexity Analysis

Time Complexity

O(maxIntervalEndingTime + n) where “n” is the number of elements in the array. First, we find the maximum Interval this cost us O(N) time. And then the creation of prefix array requires O(maxIntervalEndingTime).

Space Complexity

O(maxIntervalEndingTime) because we have been storing an array for finding how many intervals are overlapping at a particular time.

Translate »