Range sum queries without updates

Difficulty Level Easy
Frequently asked in BlackRock GE Healthcare Moonfrog Labs Synopsys Taxi4Sure Twilio
Array Larsen & Toubro Query ProblemViews 1385

Problem Statement

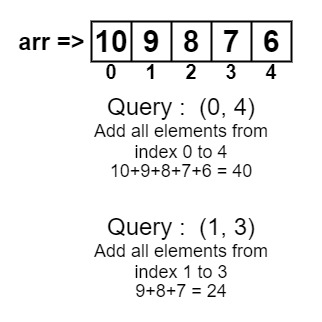
The problem “Range sum queries without updates” states that you have an array of integers and a range. The problem statement asks to find out the sum of all the elements within the given range.

Example

arr[]={10, 9, 8, 7, 6}

Query: {(0, 4), (1, 3)}
40 24

Explanation

Sum of all the numbers between the range (0, 4) inclusively is 40 and the sum of all the numbers between the range (1, 3) inclusively is 24.

Range sum queries without updates

 

Algorithm

  1. Create an array sumArray of size same as the given array.
  2. Traverse through the given array and store the sum of sumArray’s previous element and given array’s current element and store it into the sumArray.
  3. For each query, if the left is equal to 0, then return the sumArray[right],
  4. Else return the sumArray[ right ] – sumArray[left – 1].

Explanation

We have given an array of integer and a range, we have been asked to find out the sum of all the elements within the given range for each query. Each of the queries consists of a range as the start and ending point of a range. This question does not involve any update query. That means there is no need to update any of the things while finding out the query answer. We will just build the given array so that the sum of all elements from 0 index to current index is at the ith position of the built array. In this way, every query will be solved in O(1), with extra space of O(n).

We will be building the sumArray we created. In this sumArray, the sum of elements from 0 to i will be stored at the ith position of the sumArray. We will calculate this as we will add up the previous value of the sumArray and the current value of the given array and store it into the current index position of the sumArray while traversing. So when someone asked what the is the sum of all the numbers at this position, we just need to return that position’s value for every unique array elements.

When we will receive a query consisting of any range, and if we found the left or starting point of the range is equal to 0, we will just return the value of sumArray[right] that’s what we discussed above, is the left range is not equal to 0 we will return the difference of sumArray[right] and sumArray[left-1]. These will be required answers. This approach is also one of the easiest ways in which we use Dynamic Programming.

Code

C++ Code for Range sum queries without updates

#include<iostream>

using namespace std;

void buildSumArray(int arr[], int n, int sumArray[])
{
    sumArray[0] = arr[0];
    for (int i = 1; i < n; i++)
        sumArray[i] = arr[i] + sumArray[i - 1];
}

int solveQuery(int left, int right, int sumArray[])
{
    if (left == 0)
        return sumArray[right];

    return sumArray[right] - sumArray[left -1];
}

int main()
{
    int arr[] = {10,9,8,7,6};
    int n = sizeof(arr)/sizeof(arr[0]);

    int sumArray[n];

    buildSumArray(arr, n, sumArray);

    cout << solveQuery(0, 4, sumArray) << endl;
    cout << solveQuery(1, 3, sumArray) << endl;

    return 0;
}

40
24

Java code for Range sum queries without updates

class RangeQueriesSum
{
    public static void buildSumArray(int arr[], int n, int sumArray[])
    {
        sumArray[0] = arr[0];
        for (int i = 1; i < n; i++)
            sumArray[i] = arr[i] + sumArray[i - 1];
    }

    public static int solveQuery(int left, int right, int sumArray[])
    {
        if (left == 0)
            return sumArray[right];

        return sumArray[right] - sumArray[left -1];
    }

    public static void main(String[] args)
    {
        int arr[] = {10,9,8,7,6};
        int n = arr.length;

        int sumArray[] = new int[n];

        buildSumArray(arr, n, sumArray);
        System.out.println(solveQuery(0, 4, sumArray));
        System.out.println(solveQuery(1, 3, sumArray));
    }
}

40
24

Complexity Analysis

Time Complexity

O(N+Q),  because we need O(N) to compute the sumArray and then O(1) time for each query.

Space Complexity

Here in the given approach, we have created a new array sumArray to store the sum of elements from 0 to i. Thus this approach requires O(N) space. But we could have also modified the original array. Then the space complexity would have been reduced to constant.

Translate »