Count ways to reach the nth stair using step 1, 2 or 3

Difficulty Level Easy
Frequently asked in Amazon CodeNation GE Healthcare Microsoft Moonfrog Labs PayPal Uber
Combinatorial Dynamic ProgrammingViews 2624

The problem “Count ways to reach the nth stair using step 1, 2, or 3” states that you are standing on the ground. Now you need to reach the end of the staircase. So how many ways are there to reach the end if you can jump only 1, 2, or 3 steps?

Example

Count ways to reach the nth stair using step 1, 2 or 3

2
2

Explanation

There are 2 ways because either we directly reach 2nd step directly from the ground or first we reach 1st stair then move forward.

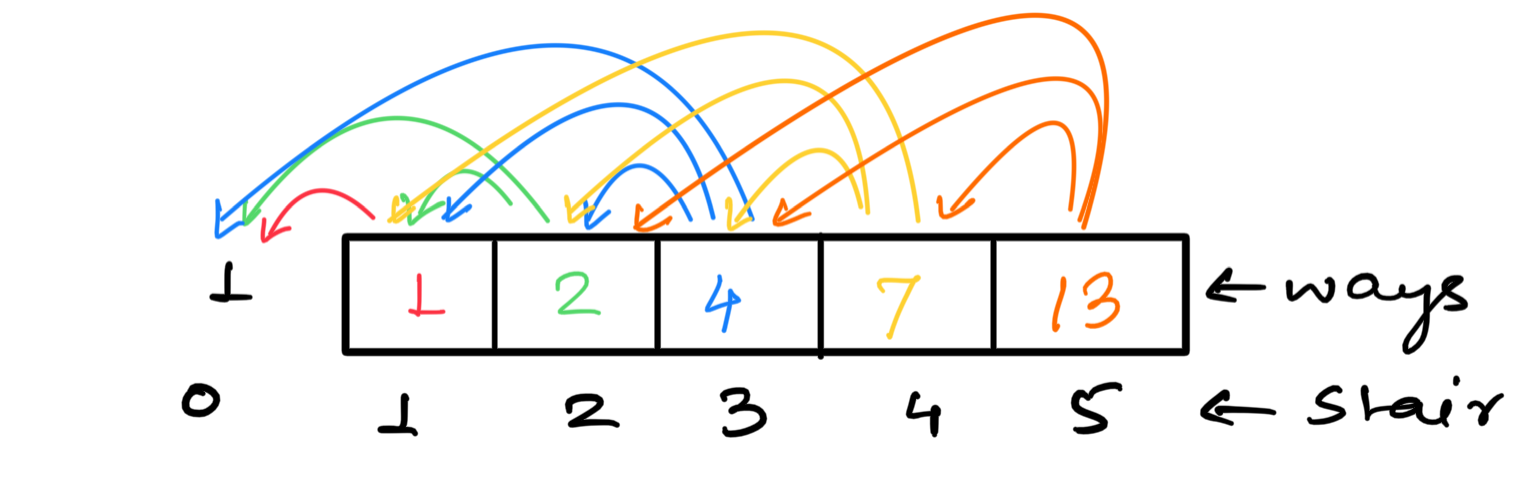
Approach

The problem asks us the total different number of ways to reach the end of the staircase such that we start from the ground. So consider the stairs has 2 steps. Then there 2 possible ways, either you step directly to 2nd step or the first step to 1st step and then to 2nd. Similarly, we need to count the ways to reach the nth stair using steps 1, 2, or 3.

A naive approach is to generate all possible ways and then count them. But this approach will be time-consuming. Thus to reduce the time complexity we must think of some different ways. The method we discussed in the naive approach is a recursive solution where you can start from the 0th step. Then in each recursive call, go to step i+1, i+2, and i+3. When you reach the nth step increment the counter. This way in the end the counter stores the number of ways to reach the nth step. But this step recomputes the same problems again and again. So to optimize this solution we use Dynamic Programming.

In the Dynamic Programming solution, we consider that we are standing at the ith step. Then the number of ways to reach ith step is from i-1 step, i-2 step, or i-3 step. So formally speaking, ways[i] = ways[i-1] + ways[i-2] + ways[i-3], using this recursive formula. We will solve our problem.

Code

C++ code to Count ways to reach the nth stair using step 1, 2 or 3

#include<bits/stdc++.h>
using namespace std;

int main(){
    int n;cin>>n;
    int dp[n+1];
    // base case
    dp[0] = 1;
    for(int i=1;i<=n;i++){
        dp[i] = ((i-1)>=0 ? dp[i-1] : 0) +
                ((i-2)>=0 ? dp[i-2] : 0) +
                ((i-3)>=0 ? dp[i-3] : 0);
    }
    cout<<dp[n];
}

5
13

Java code to Count ways to reach the nth stair using step 1, 2 or 3

import java.util.*;
class Main{
  public static void main(String[] args)
  {
    Scanner sc = new Scanner(System.in);
  int n = sc.nextInt();
    int dp[] = new int[n+1];
    // base case
    dp[0] = 1;
    for(int i=1;i<=n;i++){
        dp[i] = ((i-1)>=0 ? dp[i-1] : 0) +
                ((i-2)>=0 ? dp[i-2] : 0) +
                ((i-3)>=0 ? dp[i-3] : 0);
    }

    System.out.print(dp[n]);
  }
}
5
13

Complexity Analysis

Time Complexity

O(N), because we have to run a loop until the nth step. So in terms of Dynamic Programming, we had a single state ranging from 0 to n and the transition cost is O(1). Thus the time complexity is linear.

Space Complexity

O(N), since we need to create a 1-D DP array. The space complexity of the solution is linear.

Translate »