Minimum Sum Path in a Triangle

Difficulty Level Medium
Frequently asked in Amazon Apple Bloomberg
Array Dynamic ProgrammingViews 2581

Problem Statement

The problem “Minimum Sum Path in a Triangle” states that you are given a sequence in the form of a triangle of integers. Now starting from the top row what is the minimum sum you can achieve when you reach the bottom row?

Example

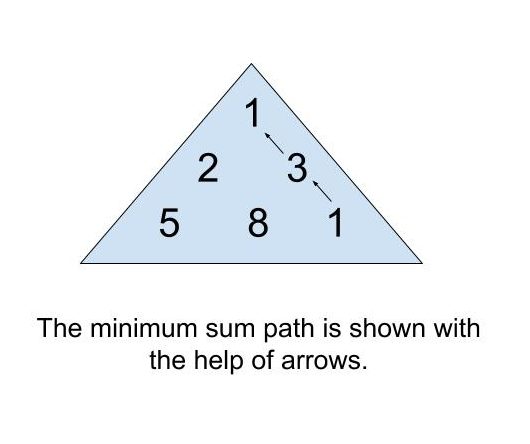
Minimum Sum Path in a Triangle

  1
 2 3
5 8 1
5

Explanation
You can simply move down the path in the following manner. 1-> 3-> 1. Thus the sum is 5. If we would have gone with a greedy approach. We would have gone with 2 instead of 3. Thus we can end up with only 8 or 11 which is greater than 5.

Approach

So how do we solve the Minimum sum path in a triangle? We have also solved a similar problem where we had to find the maximum sum path in a triangle. In that previous post, we had already discussed that the brute force approach for these problems is to generate all the paths. After the generation of these paths, just compute the sum for each of these paths and update the minimum sum.

So instead of solving this problem using brute force, we solve this with dynamic programming. Because the brute force approach is highly inefficient.

First, we fill the answer for the cells in the last row. We know that the minimum sum that can be achieved is if we start from the cells at the bottom row is the number itself. After that, we move to the row above the bottom row. For each cell in the current row, we can choose the DP values of the cells which are adjacent to it in the row just below it. And fill the minimum value which can be achieved. This way we keep on going in an upward direction. As we reach the top row, we are done with the problem.

C++ code to find Minimum path sum in a triangle

#include<bits/stdc++.h>
using namespace std;
int minimumPathSumInTriangle(vector<vector<int>> &input)
{
    int n = input.size();
    // start from row above bottom row
    // since the bottom row cells are the answers themselves
  for(int i=n-2;i>=0;i--)
  {
      // start from left to right in column
    for(int j=0;j<=i;j++)
    {
      if(input[i+1][j] < input[i+1][j+1])
        input[i][j] += input[i+1][j];
      else
        input[i][j] += input[i+1][j+1];
    }
  }
  return input[0][0];
}
int main()
{
    int n;cin>>n; // number of rows
    vector<vector<int>> input(n, vector<int>(n, 0));
    for(int i=0;i<n;i++){
        for(int j=0;j<=i;j++)
            cin>>input[i][j];
    }
    cout<<minimumPathSumInTriangle(input);
}
3
1
2 3
5 8 1
5

Java code to find Minimum path sum in a triangle

import java.util.*;
class Main{
  static int minimumPathSumInTriangle(int input[][], int n)
  {
      // start from row above bottom row
      // since the bottom row cells are the answers themselves
    for(int i=n-2;i>=0;i--)
    {
        // start from left to right in column
      for(int j=0;j<=i;j++)
      {
        if(input[i+1][j] < input[i+1][j+1])
          input[i][j] += input[i+1][j];
        else
          input[i][j] += input[i+1][j+1];
      }
    }
    return input[0][0];
  }
  public static void main(String[] args)
  {
    Scanner sc = new Scanner(System.in);
      int n = sc.nextInt(); // number of rows
      int input[][] = new int[n][n];
      for(int i=0;i<n;i++){
          for(int j=0;j<=i;j++)
              input[i][j] = sc.nextInt();
      }
      int answer = minimumPathSumInTriangle(input, n);
      System.out.print(answer);
  }
}
3
1
2 3
5 8 1
5

Complexity Analysis

Time Complexity

O(N^2), as we moved across each row and each column. In the process, we traveled to each cell. And since there were O(N^2) cells in the triangle and the transition for DP took only O(1) operation. Thus, the time complexity is also polynomial.

Space Complexity

O(N^2) since we created a 2D DP array. Thus the space complexity is also polynomial.

Translate ยป