Divisible Pairs Counting

Divisible Pairs is one of the interviewer’s favorite problem. This problem is good enough for testing interviewees’ problem skills along with knowledge on topics like arrays and hash-maps.

Problem Statement:

We have been provided with a selection of distinct positive integers.

What to find?

The number of pairs such that each element in the subset follows one rule:

1. element(i)%element(j)=0
2. element(j)%element(i)=0

i.e each element divides the other element.

Approach-1

Brute Force

Java Code For Counting Divisible Pairs

class Solution 
{
    public int largestDivisibleSubset(int[] nums) 
    {
    int count=0;
    for(int i=0;i<nums.length;i++)
    {
        for(int j=i+1;j<nums.length;j++)
        {
            if(nums[i]%nums[j]==0 || nums[j]%nums[i]==0)
                count++;
        }
    }
    return count;
    }
}

C++ Code  For Counting Divisible Pairs

class Solution
{
public:
    int largestDivisibleSubset(vector<int>& nums) 
    {
    vector<int>data;
    int count=0;
    for(int i=0;i<nums.size();i++)
    {
        for(int j=i+1;j<nums.size();j++)
        {
            if(nums[i]%nums[j]==0 || nums[j]%nums[i]==0)
                count++;
        }
    }
    return count;
    }
};

[1,2,3,9]

3

Time complexity=O(n^2)

Why?

• Two loops run in the above code
• Firstly a loop running over the array capturing the first element-O(n)
• Secondly, a loop that is running inside the first loop capturing the second element-O(n)
• In conclusion, we end up with time complexity of O(n^2)

Space Complexity=O(1)

A small tweak

What if you are asked to return the largest divisible subset out of all the subsets?

You might consider counting some consecutive pairs then and also fleeing the interview!. Worry not I’ve got your back with the easiest to do and understand the solution. Firstly I will break down the approach into four easy steps that use DP.

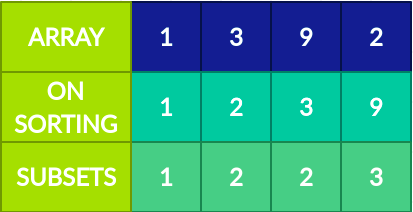
• Firstly sort the array
• Sorting the array ensures that the divisions of the array appear before it
• Secondly, create an array count
• The count array will be storing the number of divisors of a number encountered
• As we need the largest subset we loop through the counts and find the one with the largest one
• Thirdly from the element, we add the divisors thus completing the subset

As a single picture speaks for a thousand words let me illustrate the same with a picture

Java Code

class Solution
{
    public List<Integer> largestDivisibleSubset(int[] nums) 
    {
        Arrays.sort(nums);
        List<Integer>lisa=new ArrayList<Integer>();
        if(nums.length==0)
            return lisa;
        int count[]=new int[nums.length];
        int max=Integer.MIN_VALUE;
        Arrays.fill(count,1);
        for(int i=1;i<nums.length;i++)
        {
            for(int j=i-1;j>=0;j--)
            {
                if(nums[i]%nums[j]==0)
                    count[i]=Math.max(count[i],count[j]+1);
            }
        }
        int maxid=0;
        for(int i=1;i<nums.length;i++)
        {
            if(count[i]>count[maxid])
            {
                maxid = count[i] > count[maxid] ? i : maxid;
            }
        }
        int temp=nums[maxid];
        int curr=count[maxid];
        for(int i=maxid;i>=0;i--)
        {
            System.out.println(nums[i]+" "+temp+" "+count[i]);
            if(temp%nums[i]==0 && count[i]==curr)
            {
                lisa.add(nums[i]);
                temp=nums[i];
                curr--;
            }
        }
        return lisa;
    }
}

C++ Code

class Solution
{
public:
    int maxs(int a,int b)
    {
        if(a>b)
            return a;
        else
            return b;
    }
public:
    vector<int> largestDivisibleSubset(vector<int>& nums) 
    {
        sort(nums.begin(),nums.end()); 
        vector<int>lisa;
        if(nums.size()==0)
            return lisa;
        vector<int>count(nums.size(),1);
        for(int i=1;i<nums.size();i++)
        {
            for(int j=i-1;j>=0;j--)
            {
                if(nums[i]%nums[j]==0)
                    count[i]=maxs(count[i],count[j]+1);
            }
        }
        int maxid=0;
        for(int i=1;i<nums.size();i++)
        {
            if(count[i]>count[maxid])
            {
                maxid = count[i] > count[maxid] ? i : maxid;
            }
        }
        int temp=nums[maxid];
        int curr=count[maxid];
        for(int i=maxid;i>=0;i--)
        {
            if(temp%nums[i]==0 && count[i]==curr)
            {
                lisa.push_back(nums[i]);
                temp=nums[i];
                curr--;
            }
        }
        return lisa;
    }
};

Complexity Analysis For Divisible Pairs

The time complexity incurred=O(n^2)

Space we need=O(n)

Breakdown of how we reached the said time and space complexities

Space Complexity

• We create two additional spaces
• First-An array to store the results
• The maximum length of array-Length of input array=O(n)
• Second-An array to store the length of subsets
• Length of array-Length of input array=O(n)

Time Complexity

• Firstly the time incurred in sorting the array=O(n log n)
• Secondly, the time incurred in finding the subsets=O(n^2)
• How?
• We run two loops.
• The outer loop takes into account each element from the array
• The inner loop helps to add the number of divisors
• Finally, this all leads to time complexity of O(n^2)+O(nlogn)
• N^2 being bigger makes the time complexity of the entire problem O(n^2)