In the matrix chain multiplication II problem, we have given the dimensions of matrices, find the order of their multiplication such that the number of operations involved in multiplication of all the matrices is minimized.
Consider you have 3 matrices A, B, C of sizes a x b, b x c, c xd respectively. Then, if we first multiply A and B matrices and multiply their result with C. This total operation will take (a x b x c + a x c x d). If we change the order of multiplication of matrices. First, we multiply B and C matrices and then multiply their result with A. This total operation will take ( b x c x d + a x b x d ). This shows that if the order of multiplication is changed in matrices, that affects the number of operations performed. Thus, we need to find the minimum number of operation which can be done to multiply all the given matrices.
Table of Contents
Example
Input: number of matrices = 3
Dimensions of matrices = {1, 2, 3, 4}
Output: 18Explanation: First we multiply matrices with dimensions 1 x 2 and 2 x 3, which takes the cost of 6 operations. Then we multiply matrix C with the resultant matrix from the multiplication of A and B. This operation again takes 1 x 3 x 4 making a total of 18 operations.
Input: number of matrices = 2
Dimensions of matrices = {10, 10, 20}
Output: 2000Explanation: Since there are only two matrices there is only a single way of multiplying matrices which takes a total of 2000 operations.
Approach for Matrix Chain Multiplication
Matrix Multiplication Problem is one of the many standard Dynamic Programming problems. We can simply think of a recursive approach where we try all ways of multiplying matrices. We find the total cost involved in all the arrangements and take the minimum out of all arrangements. The recursive solution definitely gives us the correct result but is not efficient enough. Whenever we have a recursive solution, and we have overlapping subproblems. There is a possibility of storing the result of smaller subproblems and then combining those results to solve the initial problem. This problem has overlapping subproblems which we are being computed each time they are used. Hence, it’s more efficient if we store their result in dp table or array.
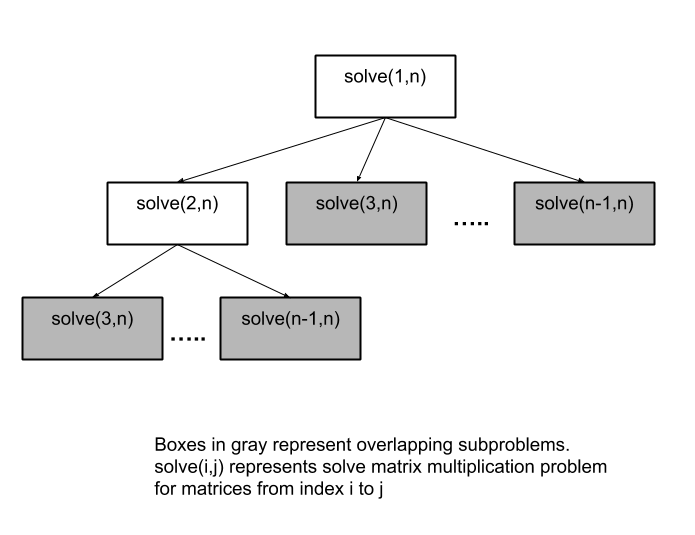
We will first solve the problem for a single matrix, which will cost 0 operations. After solving for single matrices, we solve for 2 matrices, then for 3, and so on. In a general case, consider we need to solve problems for matrices from index i to j. Since we are solving the problems in a bottom-up manner. When we solve for matrices i to j, we have computed the result for a problem with matrices i to j-1, j-2, etc. Thus, for solving this we consider that we first solve for the problem for matrices from i to k, and problem for matrices k+1 to j. Then take the minimum of all these values.
C++ Code for Matrix Chain Multiplication
#include <bits/stdc++.h>
using namespace std;
int matrixMultiplicationProblem(vector<int> matrixSize) {
int numberOfMatrices = matrixSize.size()-1;
// dp[i][j] = minimum number of operations required to multiply matrices i to j
int dp[numberOfMatrices][numberOfMatrices];
// initialising dp array with INT_MAX ( maximum number of operations )
for(int i=0;i<numberOfMatrices;i++){
for(int j=0;j<numberOfMatrices;j++){
dp[i][j] = INT_MAX;
if(i == j) // for a single matrix from i to i, cost = 0
dp[i][j] = 0;
}
}
// start solving problem for 2 matrices, then 3, and so on.
for(int len=2;len<=numberOfMatrices;len++){
for(int i=0;i<numberOfMatrices-len+1;i++){
int j = i+len-1;
for(int k=i;k<j;k++)
dp[i][j] = min(dp[i][j], dp[i][k]+dp[k+1][j]+(matrixSize[i]*matrixSize[k+1]*matrixSize[j+1]));
}
}
return dp[0][numberOfMatrices-1];
}
int main() {
int t;cin>>t;
while(t--) {
int n; cin>>n;
vector<int> matrixSize(n);
for(int i=0;i<n;i++)cin>>matrixSize[i];
cout<<matrixMultiplicationProblem(matrixSize)<<endl;
}
}
2 5 // number of inputs = dimensions of n-1 matrices 5 6 89 49 10 // dimensions of ith matrix = matrixSize[i]*matrixSize[i+1] 7 1 5 2 3 4 1000 64
26925 68028
Java Code for Matrix Chain Multiplication
import java.util.*;
import java.lang.*;
import java.io.*;
class Main {
static int matrixMultiplicationProblem(int matrixSize[]) {
int numberOfMatrices = matrixSize.length-1;
// dp[i][j] = minimum number of operations required to multiply matrices i to j
int dp[][] = new int[numberOfMatrices][numberOfMatrices];
// initialising dp array with Integer.MAX_VALUE ( maximum number of operations )
for(int i=0;i<numberOfMatrices;i++){
for(int j=0;j<numberOfMatrices;j++){
dp[i][j] = Integer.MAX_VALUE;
if(i == j) // for a single matrix from i to i, cost = 0
dp[i][j] = 0;
}
}
// start solving problem for 2 matrices, then 3, and so on.
for(int len=2;len<=numberOfMatrices;len++){
for(int i=0;i<numberOfMatrices-len+1;i++){
int j = i+len-1;
for(int k=i;k<j;k++)
dp[i][j] = Math.min(dp[i][j], dp[i][k]+dp[k+1][j]+(matrixSize[i]*matrixSize[k+1]*matrixSize[j+1]));
}
}
return dp[0][numberOfMatrices-1];
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
while(t-- > 0) {
int n = sc.nextInt();
int matrixSize[] = new int[n];
for(int i=0;i<n;i++)
matrixSize[i] = sc.nextInt();
int ans = matrixMultiplicationProblem(matrixSize);
System.out.println(ans);
}
}
}2 5 // number of inputs = dimensions of n-1 matrices 5 6 89 49 10 // dimensions of ith matrix = matrixSize[i]*matrixSize[i+1] 7 1 5 2 3 4 1000 64
26925 68028
Complexity Analysis
Time Complexity: O(N^3)
Here, we are considering two pointers i and j which are acting as bounds for matrices that run in O(N^2). The nested loop inside the outer loops itself takes linear time O(N). Thus, the algorithm runs in O(N^3) in total.
Space Complexity: O(N^2)
Since we have used a 2D dp array whose dimensions are N x N. This makes it a total of O(N^2).