Minimum number of jumps to reach end

Difficulty Level Easy
Frequently asked in Adobe Amazon Housing.com Moonfrog Labs Morgan Stanley OYO Rooms SAP Labs Walmart Labs
Dynamic Programming MathViews 3042

Problem Statement

Suppose you have an array of integers and each element of an array indicates each number as maximum jumps that can be taken from that point. Your task is to find out the minimum number of jumps to reach end, i.e. minimum of jumps that can be taken to reach the end.

Example

arr[] = {2,4,7,11,5,7,3,5}
2

Explanation: When we step on 2 it will take two steps and reach 7, it is 1 jump, and from 7 we have 5 steps and we will be at the end with 2 jumps as our answer.

2 → 7 → 5

arr[] = {1,3,2,1,3,5,1,7}
3

Explanation: With 3 jumps we can reach end 1 → 3 → 3. Here, minimum number of jumps to reach end is 3.

Algorithm for minimum number of jumps to reach end

1. Check if the first element of the array is equal to 0 if true then return -1.
2. Set the maxValue and stepTaken to the first element of the given array.
3. Set jumpTaken to 1.
4. Traverse the array from i=1 to i<n(length of the array).
  1. If the last element of the array reached, return jumpTaken.
  2. Find out the maximum value between the maxValue and arr[i] + i and store it to maxValue.
  3. Decrease the value of stepTaken by 1.
  4. If stepTaken is equal to 0.
    1. Increase jumpTaken by 1.
    2. Check if i is greater than maxValue
      Return -1.
  5. Set stepTaken to maxValue-i.
5. Return -1.

Explanation

We have given an integer array. Here, each number of the array represents the maximum steps that can be taken. There is no compulsion to take exactly those number of steps that each number represents. This means to say that suppose 6 is given then 6 steps should be taken but if in 5 steps we will be reaching an end, then it is better. We just have to find the minimum number of jumps that helps us to reach the end of the array.

We are going to do set the stepTaken and maxValue as the first element of an array. Then, we will set jumpTaken as 1 as we have to return 1 if there is the value present in an array. There is also a condition given if the first element is given as 0. It means we have nothing to step ahead so we will return just -1. Then we will traverse the array up to the length of an array. We will continue the operations until the last value of the array is reached and return the jumpTaken.

We will find the maximum value between the maxValue and the sum of i and arr[i], and decrease the value of stepTaken by 1. As we keep on decreasing the value until we find the value of stepTaken to 0. If found to be 0, then we increase the value of jumpTaken, means we have taken one or more than step to reach the end, and check if i is greater than equal to maxValue, we are going to return -1. And update the value of stepTaken to maxValue-i. We are storing this in stepTaken because until next jump we can perform maxValue- i number of steps.

As we have already declared the condition what to return and when to return, if the last element we reached while traversing, we return the jumpTaken value. And this value of jumpTaken is least number of jumps to reach end point

Minimum number of jumps to reach end

Implementation in C++ for minimum number of jumps to reach end

#include<iostream>
#include<algorithm>
using namespace std;
int getMinimumJumpTakens(int arr[], int n)
{
    if (n <= 1)
        return 0;
    if (arr[0] == 0)
        return -1;
    int maxValue = arr[0];
    int stepTaken = arr[0];
    int jumpTaken = 1;
    int i = 1;
    for (i = 1; i < n; i++)
    {
        if (i == n - 1)
            return jumpTaken;

        maxValue = max(maxValue, i + arr[i]);
        stepTaken--;
        if(stepTaken == 0)
        {
            jumpTaken++;
            if (i >= maxValue)
                return -1;

            stepTaken = maxValue - i;
        }
    }
    return -1;
}
int main()
{
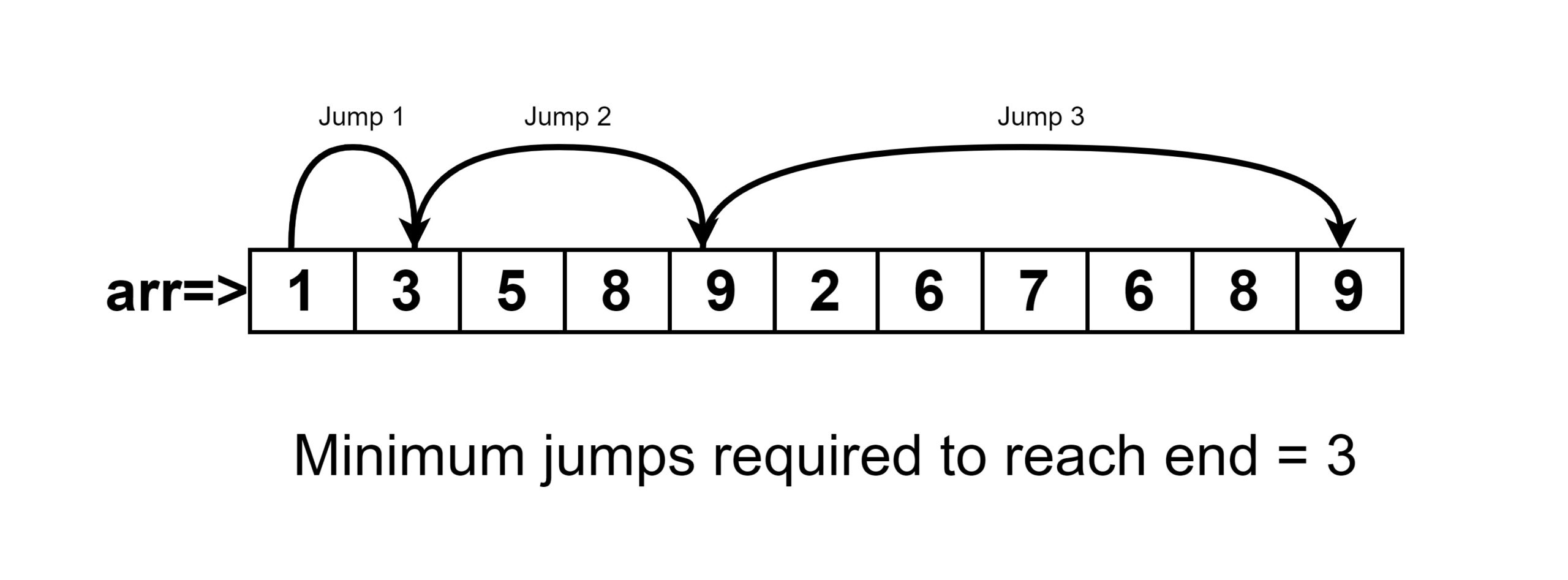
    int arr[] = { 1, 3, 5, 8, 9, 2, 6, 7, 6, 8, 9 };
    int size = sizeof(arr) / sizeof(int);
    cout <<getMinimumJumpTakens(arr, size);
    return 0;
}

3

Implementation in Java for minimum number of jumps to reach end

class MinimumJumpTakens
{
    public static int getMinimumJumpTakens(int arr[])
    {
        if (arr.length <= 1)
            return 0;

        if (arr[0] == 0)
            return -1;

        int maxValue = arr[0];
        int stepTaken = arr[0];
        int jumpTaken = 1;

        for (int i = 1; i < arr.length; i++)
        {
            if (i == arr.length - 1)
                return jumpTaken;

            maxValue = Math.max(maxValue, i + arr[i]);
            stepTaken--;
            if (stepTaken == 0)
            {
                jumpTaken++;
                if(i >= maxValue)
                    return -1;
                stepTaken = maxValue - i;
            }
        }
        return -1;
    }
    public static void main(String[] args)
    {
        int arr[] = { 1, 3, 5, 8, 9, 2, 6, 7, 6, 8, 9 };
        System.out.println(getMinimumJumpTakens(arr));
    }
}

3

Complexity Analysis

Time Complexity

O(n) where “n” is the number of elements in the array. We are traversing through the array only once, which contributes to linear time complexity.

Space Complexity

O(1) as no extra space is required. Since we have not used any extra space other than some particular number of variables, we say this algorithm has constant space complexity.

Translate »