Number of palindromic paths in a matrix

Problem Statement

We are given a two-dimensional matrix containing lowercase English alphabets, we need to count the number of palindromic paths in it. A palindromic path is nothing but a path following palindromic property. A word which when reversed remains the same as the initial word is said to be a palindrome. We need to count the number of paths from the initial point to the destination. Our starting point is the top-left cell and the destination is the bottom right corner. There is also a condition imposed on the direction of movement. We move in the right and bottom direction from the current cell.

Example

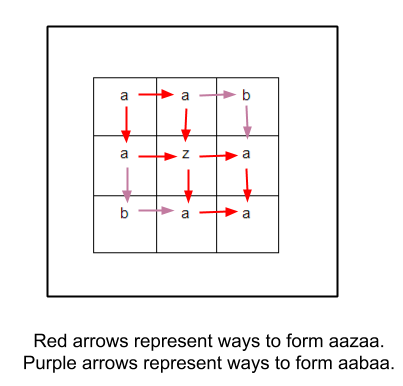
Matrix = { a a b

           a z a

           b a a }

6

Explanation: There are 6 ways to get a palindromic path from a given matrix. Because we can move from an initial point (0,0) to (0,1) and (1,0) only.

The four paths are aabaa, aazaa, aazaa, aabaa, aazaa, aazaa. The two of the paths are similar. Because the given matrix is symmetric about principal diagonal. That is the reason because we have two similar palindromic paths.

{a}

1

Explanation: Since there is only a single path “a” which is also a palindrome. The answer is 1.

Approach for number of palindromic paths in a matrix problem

Naive Approach

In this problem, we will use recursion to find all the possible sequences of paths and then check if the path is palindrome or not. The approach told before used backtracking which is not efficient enough. Since backtracking generates all possible solutions. We check all of these solutions if they are palindrome. Since this is not efficient enough we keep two variables for alphabets in the path from initial point and destination.

Efficient Approach

Now, we can summarise our algorithm. We use two variables which store the cells, one from starting and one from the end. These two stored variables should be the same for satisfying palindromic property. We move ahead if the alphabets are the same. By moving ahead, I meant we make a recursive call for subproblem in all possible directions. Whenever we have a recursive solution. We can think of dynamic programming if there are overlapping subproblems. Since we will be solving some subproblems multiple times, it is better if we store their results. We can use a map for storing the result of the subproblem. Indices of starting and ending cells serve as a key for the map. This is how we find  number of palindromic paths in a 2D array

Code for number of palindromic paths in a matrix problem

C++ Code

#include <bits/stdc++.h>
using namespace std;

// checks if index i,j is valid or not (lies inside matrix or not)
bool isValid (int n, int m, int i, int j) {
    return !(i < 0 || i >= n || j < 0 || j >= m);
}

// return number of palindromic paths in matrix
int solvePalindromicPaths(vector<vector<char>> &matrix, int startRow, int startCol, int endRow, int endCol, map<pair<pair<int,int>,pair<int,int>>,int> &dp) {
    int n = matrix.size(), m = matrix[0].size();
    
    // check if start and end cell indices are valid (are inside matrix)
    if (!isValid(n, m, startRow, startCol) || !isValid(n, m, endRow, endCol))
        return 0;
    // if start indices are after end indices, they can not meet in middle
    if (startRow > endRow || startCol > endCol)
    return 0;
    // if path does not follow palindromic property
    if (matrix[startRow][startCol] != matrix[endRow][endCol])
        return 0;
    // indices are adjacent to each other
    if (abs((startRow - endRow) + (startCol - endCol)) <= 1)
        return 1;
    // store indices as pair, since our map is using indices as key
    pair<pair<int,int>,pair<int,int>> indices = pair<pair<int,int>,pair<int,int>>
                                                (pair<int,int>(startRow, startCol), pair<int,int>(endRow, endCol));
                                                
    // if sub-problem has alredy been calculated
    if(dp.count(indices))
        return dp[indices];
        
    // if not calculated, calculate result by recursively calling in all directions
    int countOfPalindromicPaths = 0;
    countOfPalindromicPaths += solvePalindromicPaths(matrix, startRow + 1, startCol, endRow - 1, endCol, dp);
    countOfPalindromicPaths += solvePalindromicPaths(matrix, startRow + 1, startCol, endRow, endCol - 1, dp);
    countOfPalindromicPaths += solvePalindromicPaths(matrix, startRow, startCol + 1, endRow - 1, endCol, dp);
    countOfPalindromicPaths += solvePalindromicPaths(matrix, startRow, startCol + 1, endRow, endCol - 1, dp);
    
    // store and return the result
    return dp[indices] = countOfPalindromicPaths;
}

int main() {
    int t;cin>>t;
    while(t--){
        int n,m;cin>>n>>m;
        vector<vector<char>> matrix(n, vector<char>(m));
        map<pair<pair<int,int>,pair<int,int>>,int> dp;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++)
            cin>>matrix[i][j];
        }
        cout<<solvePalindromicPaths(matrix, 0, 0, n-1, m-1, dp)<<endl;
    }
}

2
2 2
a b
b a
3 3
a a b
a z a
b a a

2
6

Java Code

import java.util.*;
import java.lang.*;
import java.io.*;

class Indices {
    private int startRow;
    private int startCol;
    private int endRow;
    private int endCol;

    public Indices(int startRow, int startCol, int endRow, int endCol) {
        this.startRow = startRow;
        this.startCol = startCol;
        this.endRow = endRow;
        this.endCol = endCol;
    }
}

public class Main {

    // checks if index i,j is valid or not (lies inside matrix or not)
    static boolean isValid (int n, int m, int i, int j) {
        return !(i < 0 || i >= n || j < 0 || j >= m);
    }

    // return number of palindromic paths in matrix
    static int solvePalindromicPaths(char[][] matrix, int startRow, int startCol, int endRow, int endCol, int n, int m, HashMap<Indices, Integer> dp) {
        // check if start and end cell indices are valid (are inside matrix)
        if (!isValid(n, m, startRow, startCol) || !isValid(n, m, endRow, endCol))
            return 0;
        // if start indices are after end indices, they can not meet in middle
        if (startRow > endRow || startCol > endCol)
            return 0;
        // if path does not follow palindromic property
        if (matrix[startRow][startCol] != matrix[endRow][endCol])
            return 0;
        // indices are adjacent to each other
        if (Math.abs((startRow - endRow) + (startCol - endCol)) <= 1)
            return 1;
        // create an instance of indices with current values, since our map is using indices as key
        Indices indices = new Indices(startRow, startCol, endRow, endCol);

        // if sub-problem has alredy been calculated
        if(dp.containsKey(indices))
            return dp.get(indices);

        // if not calculated, calculate result by recursively calling in all directions
        int countOfPalindromicPaths = 0;
        countOfPalindromicPaths += solvePalindromicPaths(matrix, startRow + 1, startCol, endRow - 1, endCol, n, m, dp);
        countOfPalindromicPaths += solvePalindromicPaths(matrix, startRow + 1, startCol, endRow, endCol - 1, n, m, dp);
        countOfPalindromicPaths += solvePalindromicPaths(matrix, startRow, startCol + 1, endRow - 1, endCol, n, m, dp);
        countOfPalindromicPaths += solvePalindromicPaths(matrix, startRow, startCol + 1, endRow, endCol - 1, n, m, dp);

        // store and return the result
        dp.put(indices, countOfPalindromicPaths);
        return countOfPalindromicPaths;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int t = sc.nextInt();
        while(t-- > 0){
            int n = sc.nextInt();
            int m = sc.nextInt();
            char matrix[][] = new char[n][m];

            HashMap<Indices, Integer> dp = new HashMap<>();
            for(int i=0;i<n;i++){
                for(int j=0;j<m;j++) {
                    matrix[i][j] = sc.next().charAt(0);
                }
            }
            System.out.println(solvePalindromicPaths(matrix, 0, 0, n-1, m-1, n, m, dp));
        }
    }
}

2
2 2
a b
b a
3 3
a a b
a z a
b a a

2
6

Complexity Analysis

Time Complexity: O(N*M)

Since we are storing the result of subproblems. Because there is a total of N*M states. We have Time Complexity of O(N*M), which means number of palindromic paths in a matrix problem has polynomial time complexity.

Space Complexity: O(N*M)

Since there are just N*M states, space complexity is O(N*M).