Graph Cloning

What is Graph Cloning?

Today we have with us a reference to an undirected graph. What do we have to do? Returning a deep copy of the provided graph.

Let us look at the structure:

The Class Node:

It consists of the data value and the neighbors associated with each object of this class. There are a few methods as well to create objects/new nodes accordingly.

class Node {
    public int val;
    public List<Node> neighbors;
    
    public Node() {
        val = 0;
        neighbors = new ArrayList<Node>();
    }
    
    public Node(int _val) {
        val = _val;
        neighbors = new ArrayList<Node>();
    }
    
    public Node(int _val, ArrayList<Node> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
}

The node given to us will always be the root node. Returning a reference/copy to the root will help us return the clone of the graph we have been provided with.

Sample test case:

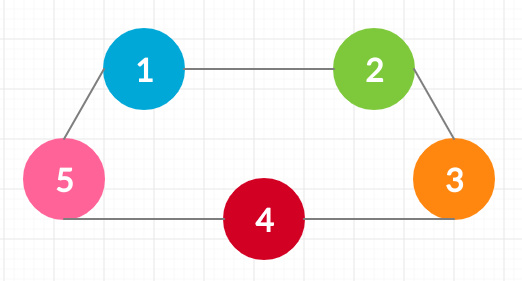
Input    :  [[1,2],[2,3],[3,4],[4,5],[1,2]]

Output :  [[1,2],[2,3],[3,4],[4,5],[1,2]]

The clone should look something like

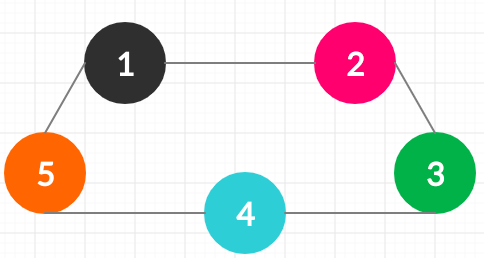
i.e consisting of the copy of the nodes which have the same values.

Disclaimer: Do not return the same graph

Solution

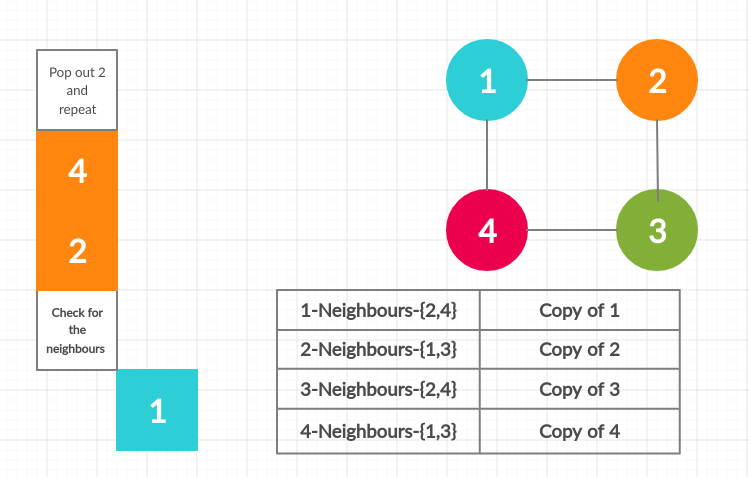
Using Breadth-First Search and HashMap

We can traverse through using BFS and maintain a HashMap for keeping a mapping of the original and the clone nodes.

Pseudocode

• Create a hashmap
• Add the root node and the copy to the hashmap
• Put the root node to the stack
• Traverse through the neighbours and keep repeating the above process
• Add the neighbours for each node
• Keep repeating the above process until the queue gets empty

For more reference lookup BFS: Breadth-First Search (BFS) for a Graph(Opens in a new browser tab)

Here is a simple image to illustrate the above process

Now that we have got a basic idea of how to do stuff let us get into the code

Java Program for Graph Cloning

class Solution 
{
    public Node cloneGraph(Node node) 
    {
     if(node==null)
         return null;
     //Creating a Queue for BFS
     Queue<Node>store=new LinkedList<Node>();
     //Adding the root node
     store.add(node);
     //Creating a hashmap of nodes and copies
     HashMap<Node,Node>hash=new HashMap<Node,Node>();
     hash.put(node,new Node(node.val));
     //Firing up the BFS!
     while(!store.isEmpty())
     {
         Node cur=store.poll();
         for(Node neigh:cur.neighbors)
         {
             if(!hash.containsKey(neigh))
             {
             hash.put(neigh,new Node(neigh.val));
             store.add(neigh);   
             }
             //Adding the neighbours to the duplicate nodes
             hash.get(cur).neighbors.add(hash.get(neigh));
         }
     }
     return(hash.get(node));
    }
}

C++ Program for Graph Cloning

class Solution 
{
public:
    Node* cloneGraph(Node* node)
    {
     if(!node)
         return NULL;
     //Creating a Queue for BFS
     queue<Node*>store;
     //Adding the root node
     store.push(node);
     //Creating a hashmap of nodes and copies
     map<Node*,Node*>hash;
     hash[node]=new Node(node->val,{});
     //Firing up the BFS!
     while(!store.empty())
     {
         Node* cur=store.front();
         store.pop();
         for(Node* neigh:cur->neighbors)
         {
             if(hash.count(neigh)==0)
             {
             hash[neigh]=new Node(neigh->val,{});
             store.push(neigh);   
             }
             //Adding the neighbours to the duplicate nodes
             hash[cur]->neighbors.push_back(hash[neigh]);
         }
     }
     return(hash[node]); 
    }
};

[[1,2],[2,3],[3,4],[4,5],[1,2]]

[[1,2],[2,3],[3,4],[4,5],[1,2]]

Complexity Analysis

Time complexity=O(V+E)

Space complexity=O(n)

V=Number of Vertices

E=Number of Edges

How did the time and space complexity end up to this?

• We have in the code a loop emptying the queue that runs over V times. In the loop
  • We remove data from the queue=O(1) operation
  • Traverse all the neighbour edges to get the clones=O(Adj)
  • Add neighbours=O(1) operation
• Summing up the complexity=V*(O(1)+O(Adj)+O(1))
• Which boils down to O(V)+O(V*Adj)
• Making the time complexity=O(V+E)
• The space complexity is O(n) as all we needed was a queue

References