Longest Span with same Sum in two Binary arrays

Difficulty Level Medium
Frequently asked in Accenture Cisco Indeed Kuliza SAP Labs Yandex
Array Hash HashingViews 1303

Problem Statement

You are given two arrays of which each contains binary number. The problem statement asks to find longest span with same sum in two binary arrays, that is to find out the maximum length common sub-array from (i, j) in such a way that j is greater than or equal to i and arr1[i] + arr1[ i + 1] + arr1[i + 2] + …. + arr1 [ j ] =  arr2[i]+arr2[i+1]+arr2[i+2]+….+arr2[j].

Example

arr1[] = {1,0,1,0,0,0,1,1}

arr2[] = {1,0,1,0,1,1,0,1}
4

Explanation: The length of the highest common span is 4 because at index 0 to 3 there is sum of both of the sub-arrays is equal.

Longest Span with same Sum in two Binary arrays

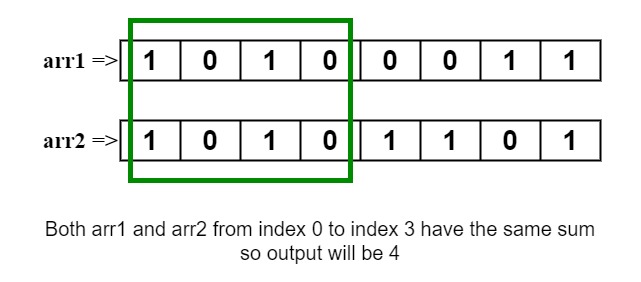
arr1[] = {1, 0, 1, 0, 1, 0}

arr2[] = {0, 1, 1, 0, 0, 0}
4

Explanation: The length of the highest common span is 4 because at index 0 to 3 there is sum of both of the sub-arrays are equal.

 

Algorithm

1. Declare an array of size n.
2. Find the difference of each element’s index of both of the arrays such that arr[i]=arr1[i]-arr2[i].
3. Declare the HashMap.
4. Set sum to 0 and maxLength to 0.
5. From i=0 to i<n.
    1. Add up the value of arr[i] and sum into the sum.
    2. Check if sum ==0, then update the maxLength=i+1.
    3. Check if the map contains the sum, then update the maxLength to the maximum between maxLength and i-key’s value.
    4. Else put the sum and its index into the map.
6. Return maxLength.

Explanation

We have given two binary arrays, each of which contains the binary number in the form of 0 and 1. We have to find the longest common span of [i,j] such that the sum of both of the arrays, in that particular span, is equal and that common span’s length of longest. For this, we are going to us the Hashing and an extra array in which we are going to store the difference of each i’th index element’s difference at the i’th position of the array created.

We create a map, in that we are going to store out the newly created array’s value as a key into the map and its index as a value. We are going to find out the maximum of that index and going to compare it with maxLength we created to find and store the maximum value as the longest length. But before that, we pick up the arr[i] and add it with arr[i] and sum and store it into the sum. We will check if the sum is equal to 0, update the maxLength to i+1. This is to handle the values at the last index element.

Check if the map contains the sum, then, update the maximum length by finding out the maximum between the maxLength and index – map[sum]. Else put the sum and index into the map. The array we made and initialized as a difference between both of the arrays plays a key role. After this, we have the value in maxLength and return the maxLength.

 

Code to find the Longest Span with same Sum in two Binary arrays

C++ code

#include<iostream>
#include<unordered_map>

using namespace std;

int longestCommonSum(int arr1[], int arr2[], int n)
{
    int arr[n];
    for (int i=0; i<n; i++)
        arr[i] = arr1[i] - arr2[i];

    unordered_map<int, int> hM;

    int sum = 0;

    int max_len = 0;
    for (int i = 0; i < n; i++)
    {
        sum += arr[i];

        if (sum == 0)
            max_len = i + 1;

        if (hM.find(sum) != hM.end())
            max_len = max(max_len, i - hM[sum]);

        else
            hM[sum] = i;
    }
    return max_len;
}

int main()
{
    int arr1[] = {0, 1, 0, 1, 1, 1, 1};
    int arr2[] = {1, 1, 1, 1, 1, 0, 1};
    int n = sizeof(arr1)/sizeof(arr1[0]);
    cout << longestCommonSum(arr1, arr2, n);
    return 0;
}

6

 

Java Code

import java.util.HashMap;

class LargestSubArr01
{
    public static int longestCommonSum(int[] arr1, int[] arr2, int n)
    {
        int[] arr = new int[n];
        for (int i = 0; i < n; i++)
            arr[i] = arr1[i] - arr2[i];

        HashMap<Integer, Integer> hM = new HashMap<>();

        int sum = 0;
        int max_len = 0;

        for (int i = 0; i < n; i++)
        {
            sum += arr[i];

            if (sum == 0)
                max_len = i + 1;

            if (hM.containsKey(sum))
                max_len = Math.max(max_len, i - hM.get(sum));

            else
                hM.put(sum, i);
        }
        return max_len;
    }
    public static void main(String args[])
    {
        int[] arr1 = {0, 1, 0, 1, 1, 1, 1};
        int[] arr2 = {1, 1, 1, 1, 1, 0, 1};
        int n = arr1.length;
        System.out.println(longestCommonSum(arr1, arr2, n));
    }
}

6

 

Complexity Analysis

Time Complexity

O(n) where “n” is the number of elements in the array. Here, we have traversed the array once, and since we have used an unordered map. Insertion, Deletion, and searching operations have O(1) time complexity. Thus, the whole algorithm for the longest span with same sum in two binary arrays has linear time complexity.

Space Complexity

Since we used the unordered_map or hash map, we have linear space complexity as well. O(n) where “n” is the number of elements in the array.

Translate »